 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод Хука - Дживса
Эффективность решения задачи (2.1) рассмотренными методами покоординатного спуска можно повысить, если дополнить описанные алгоритмы периодически повторяющимся поиском точки минимума в направлении вектора Хк-Хк" из точек Хк, k = sn, где s -количество выполненных внешних итераций. Такой подход и лежит в основе метода Хука - Дживса.
Алгоритм метода Хука -Дживса содержит две основные процедуры:
1) Исследующий покоординатный поиск в окрестности
данной точки с целью определения направления убывания
функции/(Х).
2) Перемещение в направлении убывания.
Опишем вначале алгоритм исследующего покоординатного поиска из заданной точки Хс приращениями по каждой координате Д,/= 1,...,«.
Шаг 1. Положить X = XJ = 1.
Шаг2. Сделать пробный шаг Y = ~Х ~ Д.^ ; где е > _>й ко_
ординатный вектор. Если f{Y) > f(x), то перейти к шагу 3, ина-че - к шагу 4.
Шаг 3- Сделать пробный шаг Y = ~X + h.e>. Если f(Y) > /(^), то перейти к шагу 5, иначе - к шагу 4.
Шаг 4. Положить X - Y.
Шаг 5. Положить; =;'+1". Если; < п, то перейти к шагу 2. В противном случае исследующий поиск окончен, т.е. получена
точка X, для которой /(х)</(Х),если Х*Х
В результате исследующего поиска может оказаться, что
X = X. Тогда исследующий поиск считается неудачным. Если при этом ||Л|| < е, где е - заданная точность, то полагают Х-Х. Если же заданная точность не достигнута, то полагают Д=Дд, где уе(0; 1) - коэффициент уменьшения шага, и повторяют исследующий поиск. •
Опишем теперь полный алгоритм Хука - Дживса.
ШагО. Выбрать начальную точку ХаеЕ", вектор приращений Д = (Д,,..., Д„), коэффициент уменьшения уе(0;1), параметр точности е > 0, положить к = 0.
Шаг 1. Провести исследующий покоординатный поиск из
точки Ади найти точку х\ Если Z* * Хк, то перейти к шагу 3, иначе - к шагу 2.
Шаг 2. Проверить условие достижения заданной точности ||Д||< £. Если оно выполняется, то перейти к шагу 5, иначе положить Д = Д у и перейти к шагу 1.
ШагЗ. Сделать «диагональный» шаг из точки X в направ-
лении вектора
| Провести иссл |
едующий поиск в точке ЛГи найти точ-
ку X. Если f(x)<f{?), ™ "0Л0ЖЙТЬ **=*• ^ =* и п^
рейтикшагУЗ.ИнаЧеположить^^1ДА=^ипеРейтикшагу1. Шаг 5. Завершить вычисления, положив X - X, f ~f(X).
2.2.4. Метод Пауэлла
В основе этого метода лежит рассмотренный метод покоординатного спуска Зейделя, дополненный последовательным нахождением направлений убывания после завершения очередной внешней итерации и минимизацией функцииДЛ) по этим направлениям.
Пусть задана точка начального приближения Х°еЕ ". Выполним одну внешнюю итерацию метода покоординатного спуска Зейделя (см. подразд. 2.2.2), т.е. найдем точку
2.2.5. Типовые примеры
Пример 1. Решить задачу минимизации функции двух переменных f(x) = 5xf +5x22 +8x,x2 из начальной точки Х°=(5; 5)т методом покоординатного спуска Зейделя.
Заметим, что линии уровня данной целевой функции - со-осные эллипсы с центром в начале координат, большая ось которых наклонена под углом 135° к оси х,. Результаты расчетов по приведенному в подразд. 2.2.2 алгоритму приведены в таблице и графически проиллюстрированы на рис. 2.5. При нахождении очередной точки X* минимизирующей последовательности происходит смещение по прямой, параллельной одной из координатных осей, до точки с наименьшим на этой прямой значением функции f (X). Очевидно, эта точка будет точкой касания рассматриваемой прямой и соответствующей линии уровня.
i
где е' - единичный координатный вектор, у которого /-я координата равна 1, остальные равны 0J = 1,..., „. При этом величина шага определяется с помощью какой-либо процедуры одномерной оптимизации по а:
| по а: |
одномерного
| Полагая X —X внешней итерации. "-а не выполнится |
)
анняСяТп!1аеМ К выполнению следующей
Z^£ П°Р'

Рис. 2.5. Траекюрия поиска
методом покоординатного спуска Зейделя
| к | Хх | Х2 | F(x) |
| 2 | 5 | ||
| -4 | |||
| -4 | 3,2 | 28,8 | |
| -2,56 | 3,2 | 18,43 | |
| -2,56 | 2,05 | 11,8 | |
| -1,64 | 2,05 | 7,55 | |
| -1,64 | 1,31 | 4,83 | |
| -1,05 | 1,31 | 3,09 | |
| -1,05 | 0,84 | 1,98 | |
| -0,67 | 0,84 | 1,27 | |
| -0,67 | 0,54 | 0,81 |
 Пример 2. Решить задачу минимизации функции f(X) = (*, +1)2 +4 методом Хука - Дживса из начальной точки
Пример 2. Решить задачу минимизации функции f(X) = (*, +1)2 +4 методом Хука - Дживса из начальной точки
*°=(2;3)т.
Зададим вектор перемещения А = (2; 3). Исходное значение функции в начальной точке/(ЛГ°) = 18. В соответствии с алгоритмом, описанным в подразд. 2.2.3, сначала проводим исследующий поиск из точки Х°:
^° =2 + 0,5 = 2,5; /(2,5;3) = 21,25 (неудача); xf° =2-0,5 = 1,5; /(1,5;3) = 15,25 (успех); х*1'=3 + 1 = 4; /(1,5;4) = 22,25 (неудача); xf =3-1-2; /(1,5;2) = 10,25 (успех).
Исследующий поиск оказался удачным. Теперь из новой точки Х>= (1,5; 2)т перемещаемся в направлении убывания по вектору X'-Х0 в точку X2 = IX '- Х°:
jc,<2) =2-1,5-2 = 1; xf> =2-2-3 = 1;
| = 5. |
() Проводим исследующий поиск в точке X1- (1,5; 2)т:
*,(3) =1 + 0,5 = 1,5; /(1,5;1) = 7,25>/(X2) (неудача); *,(3) =1-0,5 = 0,5; /(0,5;3) = 15,25 (успех); 4° =3 + 1 = 4; /(1,5;4) = 22,25 (неудача); 4" =3-1-2; /(1,5;2) = 10,25 (успех).
Поскольку/^3) = 2,25 </(*') = 10,25 и перемещение из точки X в точку X - (1;1) успешно, то вновь перемещаемся по направлению убывания из точки X* в точку Х*= 1ХЪ-ХХ-
проводим исследующий поиск в точке
| xf = |
=-0,5 + 0,5=0; /(0;-2) = 5 >/(**■) (неудача); = -0,5 -0,5 = -1; /(-1;-2) = 4 > /(*«) (неудача); = -2 +1 = -1; /(-0,5;-1) = 1,25 >
*•) (успех).
Поскольку/(Z5) = 1,25 </(Х3) = 2,25 и перемещение из точки Хъъ точку X4 можно признать успешным, то последовательность поисков по направлению убывания продолжаем до тех пор, пока на очередном этапе в конце исследующего поиска значение f(X) не окажется больше, чем в предыдущей точке. Тогда из последней проводим исследующий поиск для определения нового удачного направления.
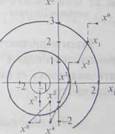
|
| Рис. 2.6. Минимизация функции методом Хука - Дживса |
На рис. 2.6 приведена графическая интерпретация этапов поиска. Линии уровня целевой функции f(X) = (x)+ 1)2 + xl - концентрические окружности с центром в точке X *=(-1; 0). Пунктиром на рисунке выделены траектории исследующего поиска, сплошными линиями - перемещения в направлении убывания. Убедитесь в соответствии графической иллюстрации описанному алгоритму.
Пример 3. Рассмотрим графическую иллюстрацию решения задачи минимизации функции'/(^) = 2х,2 +.*; -хххг методом Пау-элла из начальной точки Х°= (2; 2)т(рис. 2.7).
Линии уровня функции/(Л0 - соосные эллипсы с центром в начале координат, большая ось которых наклонена к оси х, под углом 67°,5'. Первый шаг делается в соответствии с методом покоординатного спуска Зейделя (см. рис. 2.7) из точкиХ°в направлении -е'= (-1; 0), т.е. минимизируется/^- осе') по а > 0 с помо-

|
щью процедуры одномерного поиска. В результате находится
| точка |
X' = Х°- ос,е', где а, =
= argmin|/(xo-ae1)a>O]. Оче-
видно, эта точка будет точкой касания с соответствующей линией уров-ня/(Л) = const. Аналогично выполняется второй шаг из точки X' в направлении -е2= (0;-1) и находится
„„,,, точка Х2=Х'-а,е2, где
Рис. 2.7. Минимизация функции 2
методом Пауэлла. { rl v\ г\\ г\
a, =argmm \f\X -ае J а>0>.
Затем выполняется «диагональный» шаг из точки X в направлении вектора Х2-Х°. Поскольку целевая функция/(<¥) квадратичная, точку ее минимума удается найти точно за конечное число шагов.
Порядок выполнения лабораторной работы
1. Кратко описать изучаемые методы покоординатного по
иска минимума функций многих переменных.
2. Составить алгоритм метода циклического покоординат
ного поиска.
3. Дать графическую иллюстрацию задачи индивидуально
го задания и выполнить вручную по две итерации циклического
покоординатного поиска и поиска методом Зейделя.
4. Выполнить с использованием компьютерного комплекса
расчеты индивидуальной задачи по каждому из рассмотренных
алгоритмов.
5. Провести сравнительный анализ полученных результатов.
Дать геометрическую интерпретацию решения задачи по каждо
му из алгоритмов.
6. Сформулировать выводы об эффективности изученных методов покоординатного спуска. Содержание проделанной работы отразить в отчете.
Задания для лабораторной работы
1. Минимизировать функцию/(X) = 5xf +5xj + 6х,х2
из начальной точки Х" = (2; 4)т.
| = 5x* +5x\ +8д:,х2 = 5x* +5x22 -Sxtx2 |
2. Минимизировать функцию f(X) = 5x* +5x\ -6х,х2
из начальной точки Х°= (-4; 3).
3. Минимизировать функцию f(X) = 5x* +5x\
из начальной точки Х°=(3;5)Т.
4. Минимизировать функцию
из начальной точки Х°= (-3;4)т.
5. Минимизировать функцию f(X) = 2xf +2x\ -х,*2
из начальной точкиХ°= (-1;2)т.
6. Минимизировать функцию f(X) = 2x] +2x\ +2xtx2 -
-14х, -12х, +29 из начальной точки Х° = (-1;4)т.
7. Минимизировать функцию f(X) = 2xf + 2x; -2*,х, -
-4*! -2.x, +5 из начальной точки Х°=(-1; 3)т.
8. Минимизировать функцию /(Х) = Ю0[х2 -*2) +
+ (1-.х[)~ из начальной точки X" =(-1;0)т.
2.3. Градиентные методы
Рассмотрим задачу безусловной минимизации (2.1) предполагая, что функция f(X) непрерывно дифференцируема на Е". Для численного решения задачи применим простейшую итерационную процедуру вида:
г
X"*]=Xk+akS\k= 0,1,2,..., (2.21)
позволяющую при определенных условиях построить минимизирующую последовательность для функции/(А), т.е. такую
последовательность точек Хке Е", что Jim/(jf4) = /.
От того, как выбирается направление поиска S и как определяется величина шага ак, зависят свойства итерационной процедуры (2.21) такие, как поведение функции/(^0 на элементах последовательности {X*}, сходимость к решению, скорость сходимости, объем требуемых вычислений.
Известно, что направление наибыстрейшего возрастания функции / (X) в точке X совпадает с направлением градиента функции/(А), т.е. вектора
Ж.
| дх,' |
'дх
а направление наибыстрейшего убывания - с направлением антиградиента, т.е. вектора -f'(X) Это свойство градиента и лежит в основе итерационных процедур градиентных методов, которые отличаются друг от друга лишь способом выбора величины ак градиентного шага.
Поиск по сайту: