Тема 5. Управление предпринимательскими рисками

Управление рисками представляет собой совокуп­ность приемов и методов, уменьшающих вероятность появления этих рисков или локализующих их последствия. Управление финансовыми рисками является одним из важнейших направлений деятельности финансового менеджера, требующим глубоких знаний экономики и финансов предприятий, математических и статистических методов, страхового дела и т.п. В крупных западных компаниях на управление рисками финансовый менеджер затрачивает до 45% рабочего времени.

С точки зрения своевременности принятия решения по преду­преждению и минимизации потерь можно выделить три подхода к управлению рисками:

1) активный подход означает максимальное использование ме­неджером средств управления рисками для минимизации их послед­ствий. При этом подходе все хозяйственные операции осуществляют­ся после проведения мероприятий по предупреждению возможных финансовых потерь;

2) адаптивный подход основан на учете в процессе управления сложившихся условий хозяйствования, а само управление рисками.

Коэффициент вариации (V) — относительная величина, поэтому на его размер не оказывают влияния абсолютные значения изучаемого показателя.

Он представляет собой отношение среднего квадратического отклонения к средневзвешенному значению события и определяется в процентах:

Чем больше значение коэффициента вариации, тем сильнее изменение анализируемого признака. Эмпирически установлена сле­дующая качественная оценка различных значений коэффициента вариации:

• до 10% — слабое изменение;

• от 10 до 25% — умеренное изменение;

• свыше 25% — высокое изменение.

Среднее ожидаемое значение события является средневзве­шенной величиной из всех возможных результатов с учетом вероят­ности наступления каждого результата и определяется по формуле

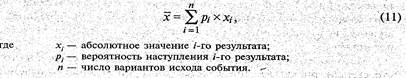
Среднее значение события представляет собой обобщенную коли­чественную характеристику и не позволяет принять решение в пользу какого-либо варианта. Для окончательного решения определить сте­пень отклонения ожидаемого значения от средней величины, мера­ми которой являются дисперсия и среднее квадратическое от­клонение

Дисперсия представляет собой среднее взвешенное из квадратов отклонений действительных результатов от средних ожидаемых:

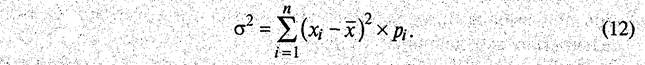
Дисперсия сигнализирует о наличии риска, но при этом не ука­зывает направление отклонения от ожидаемого значения, так как раз­ность берется в квадрате, а предпринимателю важен знак (плюс или минус) этого отклонения, чтобы знать, прибыль (+) или убыток (-) можно получить при сделке.

Среднее квадратическое отклонение определяется по формуле

Оно измеряется в тех же единицах, что и варьирующий признак.

В риск-менед­жменте получение надежной и достаточной в данных ус­ловиях информации играет главную роль, так как оно позволяет принять конкретное решение по действиям в условиях риска.

Информационное обеспечение функционирования риск-менеджмента состоит из разного рода и вида инфор­мации: статистической, экономической, коммерческой, финансовой и т. п.

Эта информация включает осведомленность о вероятно­сти того или иного страхового случая, страхового события, наличии и величине спроса на товары и капитал, финансо­вой устойчивости и платежеспособности своих клиентов, партнеров, конкурентов, ценах, курсах и тарифах, в т.ч. на услуги страховщиков, об условиях страхования, о дивиден­дах и процентах и т. п.

Тот, кто владеет информацией, владеет рынком. Многие виды информации часто составляют предмет коммерческой тайны, поэтому отдельные виды информации могут являть­ся одним из видов интеллектуальной собственности (ноу-хау) и вноситься в качестве вклада в уставный капитал ак­ционерного общества или товарищества.

Менеджер, обладающий достаточно высокой квалифи­кацией, всегда старается получить любую информацию, даже самую плохую, или какие-то ключевые моменты такой информации, или отказ от разговора на данную тему (мол­чание — тоже язык общения) и использовать их в свою пользу. Информация собирается по крупицам. Эти крупи­цы, собранные воедино, обладают уже полновесной инфор­мационной ценностью.

Наличие у финансового менеджера надежной деловой информации позволяет ему быстро принять финансовые и коммерческие решения, влияет на правильность таких ре­шений, что, естественно, ведет к снижению потерь и увели­чению прибыли. Надлежащее использование информации при заключении сделок сводит к минимуму вероятность финансовых потерь.

Любое решение основывается на информации. Важное значение имеет качество информации. Чем более расплыв­чата информация, тем неопределеннее решение. Качество информации должно оцениваться при ее получении, а не при передаче. Информация стареет быстро, поэтому ее сле­дует использовать оперативно.[4]

Хозяйствующий субъект должен уметь не только соби­рать информацию, но хранить и отыскивать ее в случае не­обходимости. В настоящее время лучшей картотекой для сбора информации является компьютер — машина, которая обладает одновременно и хорошей памятью, и возможностью (если имеются соответствующие программы) быстрее найти нужную информацию через свою кодификацию. Од­нако информационная машина выполняет решения, но" не корректирует их. Любая неправильная кодификация повле­чет за собой неправильную классификацию.

Назначение анализа риска — предоставить потенциаль­ным партнерам необходимые данные для принятия реше­ний о целесообразности участия в проекте и предусмотреть меры по защите от возможных финансовых потерь. Анализ риска производится в последовательности, приведенной на рис. 5.1.

Когда говорят в необходимости учета риска при управ­лении проектами, обычно имеют в виду основных его уча­стников: заказчика, инвестора, исполнителя (подрядчика) или продавца, покупателя, а также страховую компанию.

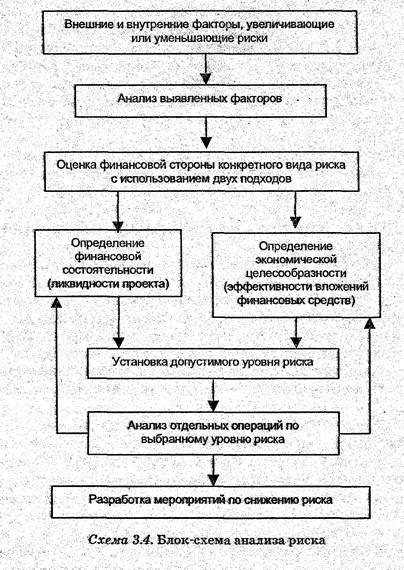
Рис.5.1. Блок-схема анализа риска

При анализе риска любого из участников проекта исполь­зуются следующие критерии, предложенные известным американским экспертом Б. Берлимером:

· потери от риска независимы друг от друга;

· потеря по одному направлению из «портфеля рис­ков» не обязательно увеличивает вероятность поте­ри по другому (за исключением форс-мажорных об­стоятельств);

· максимально возможный ущерб не должен превы­шать финансовых возможностей участника.[5]

Риск обычно подразделяется на динамический и стати­ческий.

Динамический риск — это риск непредвиденных измене­ний стоимости основного капитала вследствие принятия управленческих решений или непредвиденных изменений рыночных или политических обстоятельств. Такие измене­ния могут привести как к потерям, так и к дополнительным доходам.

Статический риск — риск потерь реальных активов вследствие нанесения ущерба собственности, а также по­терь дохода из-за недееспособности организации. Данный риск может привести только к потерям.

Анализ рисков можно подразделить на два взаимно допол­няющих друг друга вида: качественный и количественный.

Качественный анализ может быть сравнительно про­стым, его главная задача — определить факторы риска, эта­пы работы, при выполнении которых риск возникает, т. е. установить потенциальные области риска, после чего иден­тифицировать все возможные риски.

Количественный анализ риска, т. е. численное определе­ние размеров отдельных рисков и риска проекта в целом - проблема более сложная. Все факторы, так или иначе вли­яющие на рост степени риска в проекте, можно условно разделить на объективные и субъективные.

К объективным относятся факторы, не зависящие непо­средственно от самой фирмы (инфляция, конкуренция, анархия, политические и экономические кризисы, эколо­гия, таможенные пошлины и т. д.).

К субъективным относятся факторы, характеризующие непосредственно данную фирму. Это производственный потенциал, техническое оснащение, уровень предметной и технологической специализации, организация труда, уро­вень производительности труда, степень кооперированных связей, уровень техники безопасности, выбор типа контрак­тов с инвестором или заказчиком и пр. Последний фактор играет важную роль для фирмы, поскольку от типа контрак­та зависят степень риска и величина вознаграждения по окончании проекта.

Предприниматель всегда должен стремиться учиты­вать возможный риск и предусматривать меры для сниже­ния его уровня и компенсации вероятных потерь, в этом и заключается сущность управления риском. Главная цель риск-менеджмента (особенно для условий совре­менной России) — добиться, чтобы в самом "худшем слу­чае речь могла идти об отсутствии прибыли, но никак не о банкротстве.[6]

Для оценки степени приемлемости риска следует выде­лить зоны риска в зависимости от ожидаемой величины потерь. Общая картина зон риска представлена на рис.5.2.

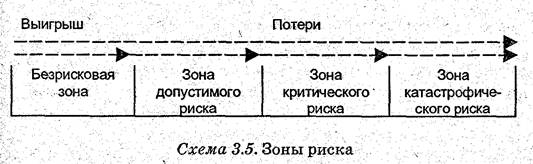
Рис.5.2. Зоны риска

Область, в которой потери не ожидаются, где экономи­ческий результат хозяйственной деятельности положитель­ный, называется безрисковой зоной.

Зона допустимого риска — область, в пределах которой величина вероятных потерь не превышает ожидаемой прибыли и, следовательно, коммерческая деятельность имеет экономическую целесообразность. Граница зоны до­пустимого риска соответствует уровню потерь, равному рас­четной прибыли.

Зона критического риска — область возможных потерь, превышающих величину ожидаемой прибыли вплоть до ве­личины полной расчетной выручки (суммы затрат и прибы­ли). Здесь предприниматель рискует не только не получить никакого дохода, но и понести прямые убытки в размере всех произведенных затрат.

Зона катастрофического риска — область вероятных потерь, которые превосходят критический уровень и могут достигать величины, равной собственному капиталу орга­низации. Катастрофический риск способен привести орга­низацию или предпринимателя к краху и банкротству. Кро­ме того, к категории катастрофического риска (независимо от величины имущественного ущерба) следует отнести риск, связанный с угрозой жизни или здоровью людей и возникновением экономических катастроф.

Наглядное представление об уровне коммерческого рис­ка дает графическое изображение зависимости вероятности потерь от их величины — кривая риска (рис.5.3.).

Рис.5.3. Кривая распределения вероятности получения прибыли

Общие закономерно­сти изменения коммерческого риска и дают возможность построить кривую распределения вероятностей потерь при­были, которую и называют кривой риска (рис.5.4).

Главное в оценке риска — возможность построения кри­вой риска и определения зон и показателей допустимого, критического и катастрофического рисков.[7]

Анализ риска основан на методологии, с помощью которой анализируется будущая неопределенность определения влияния риска на предполагаемые результаты. Для это­го математическая прогнозная модель подвергается ряду имитационных прогонов, обычно с помощью компьютера. В ходе процессов имитации строятся последовательные сценарии, где используются данные, являющиеся исходными для основных неопределенных переменных проекта.

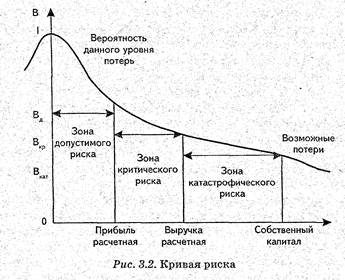
Рис.5.4. Кривая риска

Ре­зультаты имитации подвергаются статистической обработке, чтобы получить вероятностное распределение возможных результатов проекта и оценить степень риска. Таким обра­зом, процесс анализа риска включает следующие стадии:

♦ создание прогнозной модели;

♦ определение переменных риска;

♦ определение вероятностного распределения отобран­ных переменных и определение диапазона возмож­ных значений для каждой из них;

♦ установление наличия или отсутствия корреляцион­ных связей среди рисковых переменных;

♦ прогоны моделей;

♦ анализ результатов.

Переменные риска являются критическими для жизнеспо­собности проекта, т. е. даже малые отклонения от их предпо­лагаемого значения негативно отражаются на проекте.

Для отбора переменных используется анализ чувстви­тельности и неопределенности: измеряется реакция резуль­татов проекта на изменения той или иной переменной проекта. Недостаток его в том, что он не принимает во внима­ние реалистичность (или нереалистичность) предполагае­мых изменений значения анализируемых переменных. Для того чтобы результаты, полученные при анализе чувстви­тельности, имели смысл, следует учесть влияние неопреде­ленности, охватывающей переменные, подвергающиеся проверке. Например, малое отклонение в закупочной цене определенного вида оборудования в год X имеет очень боль­шое значение для дохода от проекта, но вероятность этого отклонения может быть мала, если поставщик связан опре­деленными условиями контракта. Следовательно, риск, обусловленный этой переменной, незначителен.

Анализ неопределенности помогает выделить перемен­ные повышенного риска. Причина, по которой в анализ риска включаются только наиболее важные переменные, носит двойственный характер. Во-первых, чем больше чис­ло переменных, тем выше вероятность создания неопреде­ленных сценариев; во-вторых, денежные издержки, требу­ющиеся для анализа многих переменных с малым влияни­ем на результаты, могут перевесить все возможные выгоды. Следовательно, целесообразно рассматривать ограниченное число наиболее чувствительных и неопределенных пере­менных в проекте.

Характеризуя понятие неопределенности, которое свя­зывается с данной переменной проекта, необходимо расши­рить рамки неопределенности, что позволит более или менее точно предсказать значение конкретной переменной в будущем. Совокупность предполагаемых значений пере­менной должна быть достаточно широкой, но имеющей границы: минимальное и максимальное значения. Таким образом, задается диапазон возможных значений для каж­дой рисковой переменной. Определение диапазона значе­ний переменных проекта сводится к процессу получения распределения вероятностей на основе данных, оставшихся от прежних наблюдений за какими-либо исследуемыми событиями.

Довольно редко можно позволить себе затраты на при­обретение такой количественной информации, которая позволила бы обосновать установление диапазона значений исходя из полностью объективных критериев. Чаще всего приходится полагаться на суждения и субъективные пока­затели: мнения экспертов, личные суждения, мнения лю­дей, имеющих определенные представления об объекте рас­смотрения. Установленный диапазон значений необходимо связать с распределениями вероятности, так как они дикту­ют возможность выбора значений, принадлежащих опреде­ленному диапазону. Распределение вероятности использу­ется для количественного выражения представлений и ожи­даний специалистов в отношении результатов конкретного события в будущем. [8]

Можно выделить две основные катего­рии распределения вероятности:

1) нормальное, равномерное и треугольное — разносят ве­роятность в границах одного диапазона, но с разными степе­нями концентрации относительно средних значений. Эти виды распределения называют симметричными;

2) ступенчатые и дискретные распределения, когда вы­деляются интервалы диапазона, каждому из которых при­сваивается определенный вес по вероятности ступенчатым образом (рис.5.5).

Определение рисковых переменных и придание им со­ответствующего распределения вероятности — необходи­мое условие проведения анализа рисков. При успешном завершении этих двух стадий анализа, при наличии надеж­ной компьютерной программы можно перейти к стадии моделирования.

На данной стадии компьютер вырабатывает ряд сцена­риев, основанных на случайных числах, генерируемых с использованием оговоренных распределений вероятности. Однако переход к моделированию будет справедлив толь­ко в том случае, если среди рисковых переменных, вклю­ченных в модель, будут отсутствовать какие-либо значи­мые корреляции. Две или более переменных коррелируют, если они вместе систематически изменяются.

Среди рис­ковых переменных такие отношения нередки. Наличие в модели проектного анализа коррелирующих переменных может привести к серьезным искажениям результатов анализа риска. Поэтому перед стадией прогонов модели важно убедиться в наличии или отсутствии таких связей и, где необходимо, ввести в модель ограничения, снижа­ющие вероятность появления сценариев, нарушающих такие корреляции.

Рис.5.5. Распределения вероятности с множественными значениями.

Хотя весьма редко можно объективно определить точ­ные характеристики коррелирующих переменных, в мо­дели анализа имеется возможность установить направление подобных связей и предполагаемую силу корреляции, Отношения, надлежащие описанию, основываются на ожиданиях, а не на объективных данных, поэтому очень непросто, а иногда и не нужно указывать все параметры таких отношений. Чтобы представить выработку моделью сценариев со значительным отклонением от разумного ди­апазона, достаточно принять, что отношения имеют ли­нейный характер.

Для анализа имеющихся данных обычно применяют рег­рессию и корреляцию с целью облегчить прогнозирование зависимой переменной от реальных или гипотетических зна­чений независимой переменной. В результате таких анали­зов выводятся уравнение регрессии и коэффициент корреля­ции. Для анализа рисков — это всего лишь исходные данные, а результатом является информация, выработанная в ходе моделирования. Задачей анализа корреляции применитель­но к анализу риска является контроль значений зависимой переменной, позволяющей сохранить соответствие с проти­воположными значениями независимой переменной.[9]

Статистический метод з аключается в изучении статистики потерь и прибылей, имевших место на данном или аналогичном предприятии, с целью определения вероятности события, установления величины риска. Степень, риска измеряется средним ожидаемым значением и колеблемостью возможного результата.

Среднее ожидаемое значение связано с неопределенностью ситуации, оно выражается в виде средневзвешенной величины всех возможных, результатов Е(х), где вероятность каждого результата А используется в качестве частоты или веса соответствующего значения х.

Средняя величина представляет собой обобщенную количественную характеристику и не позволяет принять решение в пользу какого-либо варианта вложения капитала. Для окончательного решения необходимо измерить изменчивость показателей, определить меру колеблемости возможного результата. Для ее определения обычно вычисляют дисперсию или среднеквадратическое отклонение.

Дисперсия представляет собой среднее взвешенное из квадратов отклонений действительных результатов от средних ожидаемых:

,

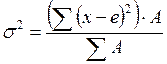где 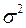- дисперсия, x - ожидаемое значение для каждого случая наблюдения, e- среднее ожидаемое значение, А - частота случаев, или число наблюдений.

Коэффициент вариации — это отношение среднего квадратичного отклонения к средней арифметической. Он показывает степень отклонения полученных значений.

,

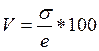где V - коэффициент вариации, - среднее квадратическое отклонение,

е - среднее ожидаемое значение

Этот коэффициент позволяет сравнивать колеблемость признаков, имеющих разные единицы измерения. Чем выше коэффициент вариации, тем сильнее колеблемость признака (до 10% - слабая колеблемость, 10—25% -умеренная колеблемость, более 25% — высокая колеблемость).

Пример: При реализации товара 1 предприятие получило прибыль 10 тыс. руб. с единицы товара в 50 случаях из 100. Вероятность 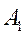=50/100=0,5.

12 тыс. руб. с единицы товара в 30 случаях из 100. =30/100=0,3.

13 тыс. руб. с единицы товара в 20 случаях из 100. =20/100=0,2.

Среднее ожидаемое значение прибыли = 10*0,5+12*0,3+13*0,2=11,2 тыс. руб.

При реализации товара 2 предприятие получило прибыль 8 тыс. руб. с единицы товара в 40 случаях из 100. Вероятность 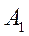=40/100=0,4.

9,5 тыс. руб. с единицы товара в 35 случаях из 100. 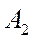=35/100=0,35.

10,5 тыс. руб. с единицы товара в 25 случаях из 100. =25/100=0,25.

=8*0,4+9,5*0,35+10,5*0,25=9.15 тыс. руб.

Для товара 1:

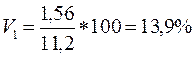
Для товара 2:

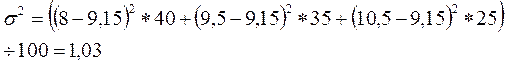
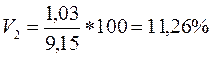
Коэффициент вариации для товара 2 меньше, чем для товара 1, значит, реализация товара 2 сопряжена с меньшим риском, она более предпочтительна.

В тех случаях, когда информация ограничена, для количественного анализа риска используются аналитические методы, или стандартные функции распределения вероятностей, например нормальное распределение, или распределение Гаусса, показательное (экспоненциальное) распределение вероятностей, которое довольно широко используется в расчетах надежности, а также распределение Пуассона, которое часто используют в теории массового обслуживания.

В зарубежной практике в качестве метода количественного определения риска вложения капитала предлагается использовать древо вероятностей.(*)

Этот метод позволяет точно определить вероятные будущие денежные потоки инвестиционного проекта в их связи с результатами предыдущих периодов времени. Если проект вложения капитала приемлем в первом периоде времени, то он может быть также приемлем и в последующих периодах времени.

Дж. К. Ван Хорн. Основы управления финансами. - М.: Финансы и статистика, 1996, с.391-392.

Необходимо измерить колеблемость показателей, т.е. определить меру изменчивости возможного результата. Колеблемость возможного результата представляет собой степень отклонения ожидаемого значения от средней величины. Для этого на практике обычно применяют два близко связанных критерия: дисперсию и среднее квадратическое отклонение. Дисперсия — среднее взвешенное из квадратов отклонений действительных результатов от средних ожидаемых

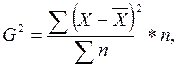
где 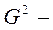дисперсия

X - ожидаемое значение для каждого случая наблюдения;

X - среднее ожидаемое значение;

n- число случаев наблюдения (частота).

Среднее квадратическое отклонение определяется по формуле:

где G- среднее квадратическое отклонение

При равенстве частот имеем частный случай

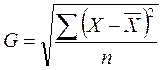
Среднее квадратическое отклонение является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Дисперсия и среднее квадратическое отклонение служат мерами абсолютной колеблемости.

Для анализа обычно используют коэффициент вариации. Коэффициент вариации представляет собой отношение среднего квадратического отклонения к средней арифметической и показывает степень отклонения полученных значений.

Поиск по сайту: