Ковариация и коэффициент корреляции

Основными понятиями, исполь­зуемыми для анализа портфеля, являются: ковариация и коэффициент корреляции. Ковариация — это мера совместной изменчивости двух активов. Например, ковариация между акциями А и В показывает, существует ли взаимосвязь между увеличением и уменьшением значения доходности этих акций, и, кроме того, показывает силу этой взаимосвязи. Ковариация между акциями A и В рассчитывается следующим образом:

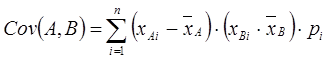(1.9)

Первый множитель в круглых скобках после знака суммы представляет собой отклонение доходности акции А от ее ожидаемого значения при i-м состоянии экономики; второй множитель — это отклонение доходности акции В для того же состояния экономики; p_i — вероятность того, что экономика будет нахо­диться в i-м состоянии; n — общее число состояний. Перед тем как перейти к примерам, отметим следующее.

1. Если значения доходности акций А и В изменяются в одинаковом напра­влении, оба множителя в скобках будут либо положительными, либо отрицательными при любом состоянии экономики; т. е. если x_Ai превышает ожидае­мое значение , то x_Bi, как правило, также будет больше, чем , и наоборот. В этом случае произведение отклонений будет положительным, тогда как при изменении значений доходности в противоположных направлениях результат будет отрицательным. Однако если колебания доходностей двух акций имеют случайный характер, их произведение будет принимать то положитель­ные, то отрицательные значения, а их сумма будет стремиться к нулю вслед­ствие взаимного погашения положительных и отрицательных величин.

2. Если доходность либо А, либо В имеет высокую степень неопределенности, ее среднее квадратическое отклонение будет достаточно большим, соответствующие множители в скобках и, следовательно, их произведения также будут большими, в результате чего абсолютное значение Cov(A,B) окажется высоким. Однако Cov(A,B) будет низкой даже в условиях, когда s_А и/или s_В относительно высоки, если колеблемость А и В является случайной, поскольку положительные и отрицательные значения в этом случае будут взаимопогашаться.

3. Если среднее квадратическое отклонение одной из акций равно нулю и, следовательно, она является безрисковой, то любое из отклонений фактической доходности от ожидаемой бу­дет равно нулю; следовательно, Cov(A,B) также будет иметь нулевое значение. Аналогичным образом, если один из активов не является абсолютно безрисковым, однако его риск сравнительно мал, соответствующие отклонения также будут небольшими, что приведет к уменьшению Cov(A,B).

Следовательно, Cov (A,B) имеет высокое положительное значение, если значения доходности двух активов изменяются однонаправленно и имеют боль­шую степень колеблемости; она имеет высокое отрицательное значение, если значения доходности изменяются в противоположных направлениях; и нако­нец, она является низкой, если колебания показателей доходности двух активов в сторону увеличения или уменьшения носят случайный характер, либо колеблемость значений одного из активов невелика.

Для иллюстрации алгоритма расчетов обратимся к данным табл. 1.3, в ко­торой приводятся распределения вероятностей доходности четырех акций.

 

Таблица 1.3

Распределение вероятностей доходности акций E, F, G и H (в %)

Вероятность	E	F	G	H
0,1	10,0	8,0	14,0	2,0
0,2	10,0	8,0	12,0	6,0
0,4	10,0	10,0	10,0	9,0
0,2	10,0	12,0	8,0	15,0
0,1	10,0	14,0	6,0	20,0
	10,0	10,0	10,0	10,0
σ	0,0	2,2	2,2	5,0

 

Используя формулу (1.9), рассчитаем ковариацию между акциями F и G:

Cov (F,G) = (6-10)(14-10)0,1+(8-10)(12-10)0,2+(10-10)(10-10)0,4+

+ (12-10)(8-10)0,2+(14-10)(6-10)0,1 = -4,8

Отрицательное значение ковариации говорит о том, что значения доходности этих акций изменяются в противоположных направлениях. Расчет ковариации между акциями F и Н дает результат Cov (F, H) = +10.8 и показывает, что доходность этих активов изменяется однонаправленно. Нуле­вое значение ковариации, например между акциями Е и F, означает, что вза­имосвязь между переменными отсутствует, т. е. они независимы (доходность Е всегда равна 10 %, следовательно, s_E=0 %, поэтому ковариация Е с любой другой акцией должна быть равна нулю).

Содержательно интерпретировать численное значение ковариации доста­точно сложно, поэтому очень часто для измерения силы связи между двумя переменными используется другая статистическая характеристика, называемая коэффициентом корреляции. Этот коэффициент позволяет стандартизировать ковариацию путем деления ее на произведение соответствующих средних квадратических отклонений и привести величины к сопоставимому виду. Коэф­фициент корреляции между переменными А и В рассчитывается следующим образом:

(1.10)

Знак коэффициента корреляции совпадает со знаком ковариации, поэтому положительная его величина означает однонаправленное изменение переменных, а отрицательная - их изменение в противоположных направлениях. Если значение r близко к нулю, связь между переменными слабая. Кроме того, процедура стандартизации приводит к тому, что коэффициент корреляции принадлежит интервалу от –1.0 до +1.0. Отметим также, что формула (1.10) может использоваться для расчета ковариации

(1.11)

 

Используя (1.10), находим, что коэффициент корреляции между акциями F и G равен -1.0 (не учитывая ошибку округления). Можно сказать, что между этими акциями имеет место обратная функциональ­ная связь. Коэффициент корреляции между акциями F и H составляет -0.9. Таким образом, между ними существует сильная прямая взаимосвязь.

 

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

---