 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Анализ общего риска: активы, рассматриваемые изолированно
Понятия распределения вероятностей и ожидаемой величины могут использоваться как основа для измерения риска. Однако каким образом можно измерить риск и оценить его количественно? Чтобы ответить на этот вопрос, вспомним основные понятия экономической статистики: «дисперсия» и «среднее квадратическое отклонение».
Дисперсией называется мера разброса возможных исходов относительно ожидаемого значения: чем выше дисперсия, тем больше разброс. Для расчета дисперсии дискретного распределения используется следующая формула (1.2):
 (1.2)
(1.2)
Как показывает (1.2), дисперсия есть сумма квадратов отклонений от среднего ожидаемого значения, взвешенная на вероятность появления каждого отклонения. Рассчитаем, например, дисперсию доходности проекта 2 по данным табл. 1.1.
Таблица 1.1
Оценка доходности по четырем инвестиционным альтернативам
| Состояние экономики | Вероятность | Казначейские векселя, % | Доходность инвестиций при данном состоянии экономики, % | ||
| Корпоративные облигации | Проект 1 | Проект 2 | |||
| Глубокий спад Незначительный спад Стагнация Незначительный подъем Сильный подъем | 0,05 0,20 0,50 0,20 0,05 | 8,0 8,0 8,0 8,0 8,0 | 12,0 10,0 9,0 8,5 8,0 | -3,0 6,0 11,0 14,0 19,0 | -2,0 9,0 12,0 15,0 26,0 |
| Ожидаемая доходность | - | 8,0 | 9,2 | 10,3 | 12,0 |
Нам известно, что ожидаемая доходность проекта,  , равна 12.0 %. Следовательно, расчет дисперсии по формуле (1.2) и данным табл. 1.1 производится следующим образом:
, равна 12.0 %. Следовательно, расчет дисперсии по формуле (1.2) и данным табл. 1.1 производится следующим образом:
s 2= (-2.0 - 12.0)2 0.05 + (9.0 - 12.0)2 0.20 + (12.0 - 12.0)2 0.50 + (15.0 - 12.0)2 0.20 + + (26.0 - 12.0)2 0.05 = 23.2.
Дисперсию измеряют в тех же единицах, что и исходы, в данном случае в процентах в квадрате.
Поскольку интерпретация термина «процент в квадрате» затруднительна, в качестве другого измерителя разброса индивидуальных значений вокруг среднего часто используется среднее квадратическое отклонение, представляющее собой квадратный корень из дисперсии (1.3):
 (1.3)
(1.3)
Так, среднее квадратическое отклонение доходности проекта 2 равно s = 4.82 %.
Используя этот показатель в качестве меры разброса, можно сделать ряд полезных выводов о распределении исходов. В частности, если распределение является непрерывным и близким к нормальному, можно утверждать, что 68.3 % всех исходов лежит в пределах одного среднего квадратического отклонения от ожидаемого значения, 99.5 % — в пределах двух средних квадратических отклонений и практически все исходы (99.7 %) — в пределах трех средних квадратических отклонений. Даже если распределение не является близким к нормальному, на основании теоремы Чебышева можно утверждать, что для любогораспределения не менее 89 % всех исходов лежит в пределах трех средних квадратических отклонений от ожидаемого значения.
Таблица 1.2
Оценка доходности и риска четырех инвестиционным альтернативам
| Показатель | Варианты инвестирования | |||
| казначейские векселя | корпорационные облигации | проект 1 | проект 2 | |
1. Ожидаемая доходность ( ), % ), %
| 8,00 | 9,20 | 10,30 | 12,00 |
2. Дисперсия ( ) )
| 0,00 | 0,71 | 19,31 | 23,20 |
3. Среднее квадратическое отклонение ( ), % ), %
| 0,00 | 0,84 | 4,39 | 4,82 |
| 4. Коэффициент вариации (Kv) | 0,00 | 0,09 | 0,43 | 0,40 |
В табл. 1.2 приводятся ожидаемые значения доходности, дисперсия и среднее квадратическое отклонение по всем четырем альтернативным вариантам инвестирования, а также коэффициент вариации, который мы рассмотрим позднее. Видно, что казначейские векселя обладают наименьшими значениями показателей дисперсии и среднего квадратического отклонения, а проекту 2 соответствуют наибольшие их значения.
По данным табл. 1.2 можно, казалось бы, прийти к заключению, что казначейские векселя — наименее рисковый вариант инвестирования, а проект 2 — наиболее рисковый. Однако это не всегда верно; перед тем как сделать окончательный вывод, необходимо принять во внимание ряд других факторов, таких как численные значения ожидаемой доходности, асимметрия распределения, достоверность наших оценок распределения вероятностей и взаимосвязь каждого актива с другими активами, включенными в портфель инвестиций. Анализируя риск, логично сосредоточиться в основном на вероятностях тех значений доходности, которые меньше ожидаемого значения, а не на тех, которые его превышают. Если распределение является симметричным, и дисперсия и среднее квадратическое отклонение будут точно измерять риск получения доходности ниже ожидаемого значения, который составляет ровно половину общего риска. Однако если распределение асимметрично, эти показатели неверно отражают действительный риск. Если распределение обладает правосторонней асимметрией, дисперсия и среднее квадратическое отклонение завышают риск получения доходности ниже ожидаемого значения, а если распределение имеет левостороннюю асимметрию, наблюдается противоположная ситуация. Статистической характеристикой, элиминирующей эти искажения, является полудисперсия (semivariance, SV), которая определяется по формуле (1.4)
 (1.4)
(1.4)
где m — множество исходов, которые лежат нижеожидаемого значения.
Если распределение симметрично, то полудисперсия составляет половину дисперсии. Это верно для проекта 2. Однако полудисперсия проекта 1 составляет более половины дисперсии — поскольку распределение доходности проекта 1 имеет левостороннюю асимметрию, его дисперсия занижает риск получения доходности ниже ожидаемого значения. Полудисперсия корпорационных облигаций меньше половины дисперсии — поскольку распределение доходности имеет правостороннюю асимметрию, его дисперсия завышает риск получения доходности ниже ожидаемого значения. Финансовая статистика, как правило, недостаточно точна, чтобы применять к ней высокоточные аналитические методы, а большинство распределений близко к симметричным, поэтому остановимся на дисперсии и среднем квадратическом отклонении как мерах разброса.
Как правило, чем выше ожидаемая доходность, тем больше величина среднего квадратического отклонения. Предположим, например, что ожидаемая доходность проекта X составляет 30 %, среднее квадратическое отклонение – 10 %, а ожидаемая доходность проекта Y равна 10 %, среднее квадратическое отклонение — 5 %. Если распределение доходности проектов приблизительно нормальное, вероятность того, что доходность проекта X окажется отрицательной, очень мала, несмотря на то, что его среднее квадратическое отклонение равно 10 %, в то время как для проекта Y, значение s которого в два раза меньше по сравнению с проектом X, вероятность убытков будет значительно выше. Следовательно, прежде чем использовать sв качестве меры относительного риска инвестиций с различной ожидаемой доходностью, необходимо стандартизировать среднее квадратическое отклонение и рассчитать риск, приходящийся на единицу доходности. Сделать это можно при помощи коэффициента вариации, который представляет собой отношение среднего квадратического отклонения к ожидаемому значению доходности:
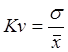 (1.5)
(1.5)
Проект X: Kvx = 10 %: 30 % =0.33, проект Y :Kvy = 5 %: 10 % =0.50.
Таким образом, видно, что на самом деле по проекту Y риск на единицу ожидаемой доходности больше по сравнению с таковым проекта X. Следовательно, можно утверждать, что проект Y является более рисковым, чем проект X, несмотря на то, что среднее квадратическое отклонение для проекта X выше, чем для проекта Y.
В 4-й строке табл. 1.2 приведены значения коэффициентов вариации для четырех исходных вариантов инвестирования. Как следует из данных таблицы, классификация проектов по коэффициенту вариации как мере риска отличается от классификации, основанной на измерении риска с помощью s: проект 2 является более рисковым, чем проект 1, по критерию среднего квадратического отклонения, а после корректировки различий в доходности и измерения риска с помощью коэффициента вариации вывод будет прямо противоположным.
2.2. Субъективные и объективные распределения вероятностей
Во всех предыдущих примерах при построении распределений вероятностей использовались субъективные оценки риска и доходности в будущем. Те же методы можно применять и к фактическим данным для получения объективных, а не субъективных оценок риска, при условии, что имеются в наличии временные ряды данных. Например, предположим, что инвестиции, аналогичные инвестициям проекта 2, осуществлялись ежегодно в течение последних 10 лет. В данном случае имеется 10 фактических значений доходности, x, этого проекта. Эти значения можно использовать для расчета динамическихсредних значений доходности, дисперсии и среднего квадратического отклонения для проекта 2:
 (1.6)
(1.6)
Эти формулы обычно используются для анализа выборочных данных, а не исходные данные рассматриваются как выборка из более крупной совокупности. Использование временных рядов в прогнозных целях основывается на предпосылке, что существующие тенденции сохранятся и в будущем. Если это так, временные ряды можно использовать как основу для составления прогнозов, а полученные средние значения доходности, дисперсии, среднего квадратического отклонения и коэффициента вариации - для оценки проекта 2. Совершенно очевидно также, что такой анализ неприменим для оценки новых проектов - если нет соответствующих временных рядов данных, необходимо основываться на субъективных оценках вероятностей. Но главное, что стоит помнить, анализируя риск, можно производить абсолютно точные расчеты, однако на самом деле они в значительной степени субъективны.
2.3 Анализ рыночного риска: активы, входящие в портфель
Рассмотрим оценку рисковости активов, объединенных в портфель, в том числе и при различном их сочетании. Как будет показано ниже, актив, входящий в портфель, обычно является менее рисковым, чем если бы он был изолирован. Действительно, актив, имеющий сам по себе высокий уровень риска, может оказаться безрисковым, если он входит в портфель, состоящий из большого числа различных активов.
Ожидаемая доходность портфеля представляет собой взвешенную среднюю из показателей ожидаемой доходности отдельных ценных бумаг, входящих в данный портфель (1.7):
 (1.7)
(1.7)
где  — ожидаемая доходность портфеля; wi — доля портфеля, инвестируемая в i-й актив; xi — ожидаемая доходность i-гo актива; n — число активов в портфеле. Например, предположим, что ожидаемая доходность акций АxA = 10 %, а акций В xB = 15 %. Если весь капитал вложить в акции А, ожидаемая доходность портфеля xp = xA = 10 %. Если инвестировать капитал только в акции В, ожидаемая доходность инвестиций составит xp = xB = 15 %. При инвестировании капитала в акции равными долями ожидаемая доходность портфеля будет равна средневзвешенной из доходностей акций: xp = 0.5*10 % + 0.5*15 % = 12.5 %. По истечении года фактические значения доходности акций А и В, а следовательно и портфеля в целом, возможно, будут не совпадать с их ожидаемыми значениями.
— ожидаемая доходность портфеля; wi — доля портфеля, инвестируемая в i-й актив; xi — ожидаемая доходность i-гo актива; n — число активов в портфеле. Например, предположим, что ожидаемая доходность акций АxA = 10 %, а акций В xB = 15 %. Если весь капитал вложить в акции А, ожидаемая доходность портфеля xp = xA = 10 %. Если инвестировать капитал только в акции В, ожидаемая доходность инвестиций составит xp = xB = 15 %. При инвестировании капитала в акции равными долями ожидаемая доходность портфеля будет равна средневзвешенной из доходностей акций: xp = 0.5*10 % + 0.5*15 % = 12.5 %. По истечении года фактические значения доходности акций А и В, а следовательно и портфеля в целом, возможно, будут не совпадать с их ожидаемыми значениями.
Как было отмечено, ожидаемая доходность портфеля представляет собой средневзвешенную из ожидаемых доходностей отдельных акций, входящих в портфель, а вклад каждой акции в ожидаемую доходность портфеля равен (wi*xi).. Что касается средних квадратических отклонений портфеля, s р, и составляющих его ценных бумаг, то они подобным алгоритмом уже несвязаны. Теоретически можно подобрать две акции, каждая из которых имеет высокий уровень риска, характеризуемый показателем среднего квадратического отклонения, и составить из этих высокорисковых активов портфель, который окажется абсолютно безрисковым, т. е. s р = 0 %. Чтобы проиллюстрировать сказанное, рассмотрим пример, приведенный на рис. 1, где показаны фактические значения доходности акций W и M, а также портфеля, в который эти две акции входят равными долями (акции получили названия W и М, поскольку графики их доходности сходны с написанием этих букв). Каждая из акций имеет среднее квадратическое отклонение si = 22.6 % и, будучи рассмотренной изолированно, является высокорисковой. Из акций W и М можно составить безрисковый портфель, поскольку показатели их доходности изменяются в противоположных направлениях: когда доходность W уменьшается, доходность М возрастает, и наоборот. Если говорить языком статистики, между показателями доходности акций W и М имеет место обратная функциональная связь, т. е. коэффициент корреляции r = - 1.0.
График доходности портфеля W, М (по данным рисунка 1) не имеет отклонений, т.е. sp= 0. Таким образом, при объединении рассматриваемых акций в портфель произошла диверсификация риска инвестора. Это стало возможным из-за наличия обратной функциональной связи между составляющими портфеля.
Поиск по сайту: