АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Портфель, состоящий из двух активов

Читайте также:
  1. Анализ динамики активов, состава и структуры активов.
  2. Анализ краткосрочных активов.
  3. Анализ состава и движения собственного капитала. Оценка чистых активов.
  4. Анализ структуры и динамики внеоборотных активов.
  5. Вопрос 27 Сущность и виды финансового риска. Риск и доходность финансовых активов.
  6. Документальное оформление и учет поступления нематериальных активов.
  7. Инспектирование представляет собой изучение записей, документов и (или) материальных активов.
  8. Комплексная оценка эффективности деятельности на основе пятифакторной модели рентабельности активов.
  9. Моделирование выбора стратегии финансирования оборотных активов.
  10. Оборачиваемость оборотных активов. Понятие операционного и финансового циклов
  11. Операционный и денежный циклы. Принцип оптимизации оборотных активов.
  12. Основные факторы и пути повышения рентабельности активов.

Если предположить, что распределе­ния доходности отдельных ценных бумаг являются нормальными, то для определения риска портфеля, состоящего из двух активов, может использоваться следующая формула, весьма громоздкая по виду, но достаточно удобная в вы­числительном плане:

(1.12)

где wA — доля портфеля, инвестируемая в ценную бумагу А, следовательно wB — доля портфеля, инвестируемая в ценную бумагу В.

Если в данную формулу включить дополнительные слагаемые, ее можно использовать для любого числа активов, входящих в портфель.

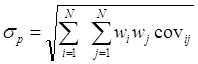(1.13)

 

3. Эффективные портфели

Одним из важнейших применений статистических методов измерения взаи­мосвязей является выбор эффективных портфелей, т. е. таких портфелей, ко­торые обеспечивают максимальную ожидаемую доходность при любом уровне риска или минимальный уровень риска для любой ожидаемой доходности. Чтобы проиллюстрировать это понятие, предположим, что необходимо вложить капитал в ценные бумаги А и В, причем распределение капитала между этими ценными бумагами может быть любым. Предположим далее, что ожидаемая доходность ценной бумаги A - 5 %, среднее квадратическое отклонение до­ходности - 4 %, тогда как xВ = 8 % и sВ = 10 %. Первоочередная задача состоит в том, чтобы определить множество допустимых портфелей и затем выделить из допустимого множества эффективное подмножество.

Для определения допустимого множества нужно иметь данные об уровне корреляции между показателями ожидаемой доходности двух ценных бумаг

(rA,B). Рассмотрим три возможных значения коэффициента корреляции:

rA,B = +1.0, rA,B = -1.0 и rA,B = 0, и вычислим по этим значениям ожи­даемую доходность и среднее квадратическое отклонение портфеля (в действи­тельности, естественно, будет только одно значение коэффициента корреляции: но в примере рассматриваются три альтернативных варианта, которые могут иметь место).

В табл. 1.4 приведены значения xp и sр. На рис. 2 представлены график xp, sр и допустимого множества портфелей для каждого значения коэффициента корреляции.

 

Таблица 1.4

Значения xp и sp при различных сочетаниях активов

1,000,00

Доля ценных бумаг А в портфеле Доля ценных бумаг В в портфеле Вариант 1 (rA,B = +1,0) Вариант 2 (rA,B = 0) Вариант 3 (rA,B = –1,0)
, % , % , % , % , % , %
5,00 4,0 5,00 4,0 5,00 4,0
0,75 0,25 5,75 5,5 5,75 3,9 5,75 0,5
0,50 0,50 6,50 7,0 6,50 5,4 6,50 3,0
0,25 0,75 7,25 8,5 7,25 7,6 7,25 6,5
0,00 1,00 8,00 10,0 8,00 10,0 8,00 10,0

 

При анализе данных таблицы и графиков следует принимать во внимание следующее.

1. Три графика в верхней части рис. 2 соответствуют варианту прямой функциональной связи между двумя активами с rAB = +1.0. Три графика в середине рис. 2 соответствуют варианту независимости активов, когда коэффициент корреляции равен нулю, а три графика в нижней части рисунка – варианту обратной функциональной связи.

2. Все три варианта являются теоретическими в том смысле, что на практике они встречаются чрезвычайно редко. В реальной действительности rAB для большинства акций находится в пределах от +0.5 до +0.7. Графики, соответствующие варианту 2, наиболее близки к реальным примерам с точки зрения формы представленных на них кривых.

3. При рассмотрении рис. 2 в вертикальном разрезе левый ряд графике: (рис. 2, (а))характеризует изменение ожидаемой доходности портфеля в зависимости от различных сочетаний А и В. Видно, что в каждом случае эти графики абсолютно идентичны: доходность портфеля есть линейная функция от доли акций в портфеле и не зависит от значений коэффициента корреляции активов портфеля.

 

а) б) в)

 

 

% % σВ = 10% , %

 

Вариант 1 = 8% В

rA,B = +1,0 σР А

= 5% kР σA = 4%

 

100% А 100% В 100% А 100% В σР,%

 

% % ,%

σВ = 10%

Вариант 2 = 8% B

rA,B = 0 σР Y

= 5% kР σA = 4% А

 

100% А 100% В 100% А 100% В σР,%

 

% % σВ = 10% ,%

Вариант 3 kВ = 8%

rA,B = -1,0 σР Y B

kA = 5%

kР σA = 4% А

 

 

100% А 100% В 100% А 100% В σР,%

 

Рисунок 2. Доходность и риск портфеля при различном сочетании активов.

а – доходность; б – риск; в – взаимосвязь риска и доходности.

 

4. Рис. 2, (б)характеризует влияние на риск структуры портфеля. Видно, что риск портфеля s р является линейным в варианте 1 при rAB = +1.0, но он нелинеен в варианте 2, а в варианте 3 для rAB = -1.0 может быть полностью сведен к нулю. Таким образом, sр в отличие от xp зависит от коэффициента корреляции.

5. На рис. 2, (в) показано допустимое, или возможное, множество портфелей, имеющих различную структуру. По данным табл. 1.4 на каждый из трех графиков были нанесены значения пар точек xp и sр. Если рассматривать только две ценные бумаги, допустимое множество будет представлять собой отрезок кривой или прямой, причем любая комбинация риска и доходности на соответствующей кривой может быть получена путем распределения денежных средств между ценными бумагами А и В.

6. Являются ли все портфели, принадлежащие допустимому множеству, в равной степени хорошими? Ответ однозначен: нет. Только часть допустимого множества, лежащую в вариантах 2 и 3 между точками Y и В, можно считать эффективной. Участок между точками А и Y не является эффективным, поскольку при любом уровне риска на отрезке AY можно получить более высо­кую доходность, принадлежащую отрезку YВ. Таким образом, ни у одного рационального инвестора не будет портфеля, принадлежащего отрезку АY. Однако в варианте 1 все допустимое множество является эффективным — ни одно из сочетаний ценных бумаг не может быть исключено из рассмотре­ния.

Из приведенных примеров следует, что в одном из экстремальных случаев (r = -1.0) риск может быть полностью элиминирован, тогда как в другом экстримальном случае (r = +1.0) диверсификация не приводит к каким-либо улучшениям. Во всех остальных случаях объединение двух акций в портфель ведет к снижению риска отдельных акций, однако не устраняет его полностью.

На рисунке 3 построена кривая ожидаемой доходности и риска, достижимых при разных комбинациях двух видов акций. Какая из комбинаций лучшая? Это всецело зависит от ваших вкусов. Если вы желаете все поставить на карту ради быстрого обогаще­ния, вам лучше вложить все деньги в Reebok. Если же вы предпочитаете более спокой­ную жизнь, основную часть денег стоит инвестировать в Coca-Cola; для минимизации риска вам следует держать в акциях Reebok лишь небольшую часть своих инвестиций.

Рис. 3. кривая ожидаемой доходности и риска, достижимых при разных комбинациях двух видов акций.

 

 
 

На практике ничто не заставляет вас ограничиваться инвестициями всего лишь в два вида акций. Допустим, вы можете составить портфель из любых акций, перечис­ленных в первом столбце таблицы 1.5. Изучив перспективы каждой фирмы, вы прогно­зируете доходность их акций так, как это показано во втором столбце таблицы. На основе данных за последние пять лет вы оцениваете риск каждого вида акций (стол­бец 3) и корреляцию доходностей в любой паре акций.

Если бы вы инвестировали 65 % ваших денег в Coca-Cola и 35 % в Reebok, ожидаемая доход­ность такого портфеля, равная 13,5 %, — это просто средневзвешенная ожидаемых до­ходностей двух видов акций. А как обстоят дела с риском такого портфеля? Мы уже знаем, что благодаря диверсификации портфельный риск меньше, чем средняя рисков отдельных акций. Так и есть: данные за прошлые периоды показывают, что среднее квадратическое отклонение этого портфеля равно 31,7 %.

 

 

Таблица 1.5 Образцы эффективных портфелей, подобранных из акций 10 фирм (числовые данные в %)  
Название фирмы Доходность, % Риск, % Эффективные портфели (доля каждого вида акций в общем составе)
                   
А   Б   В   Г
                 
Amazon. com 34,6 110,6     9,3   4,5   —
Boeing 13,0 30,9 —   2,1   9,6   0.6
Coca-Cola 10,0 31,5 —   —   _   0,4
Dell Computer 26,2 62,7 —   21,1   14,4   —
Exxon Mobil 11,8 17,4 —   —   3,6   56,3
General Electric 18,0 26,8 —   46,8   39,7   10,2
General Motors McDonald's 15,8 14,0 33,4 27,4 — —   — —   — 5,4   9,0 10,0
Pfizer 14,8 29,3 —   —   9,8   13,3
Reebok 20,0 58,5 —   20,7   13,0   —
Ожидаемая доходность Портфеля, %   34,6   21,6   19,0   13,4
Среднее квадратическое отклонение Портфеля, % 110,6   30,8   23,7   14,6
         

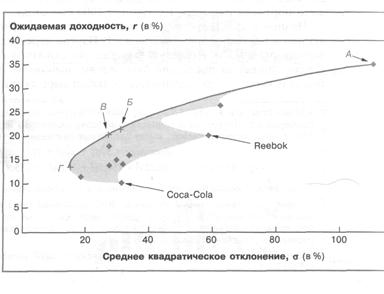
Давайте теперь обратимся к рисунку 4. Каждый ромбикобозначает комбинацию риска и доходности, характерную для ценных бумаг отдельной фирмы. Скажем, акции Amazon. com отличаются наивысшим средним квадратическим отклонением, но онисулят и самую высокую ожидаемую доходность. На это указывает ромбик в правойверхней части рисунка. Составляя инвестиционные портфели из разных ценных бумаг, вы можете получить еще более широкий выбор сочетаний риска и ожидаемой доходности: по сути, вам доступна любая комбинация в заштрихованной области на рисунке 4. Но какая же точка (комбинация риска и доходности) в этой области наилучшая? Ответ очевиден: вам хотелось бы двигаться вверх (к более высокой ожидаемой доходности) и влево (к более низкому риску).

 
 

Следуйте этим курсом до тех пор, пока это в ваших возможностях и, в конце концов, получите один из портфелей, расположенных на сплошной кривой. Гарри Маркович, в своих исследованиях в 1952, назвал их эффективными портфелями. Такие портфели, безусловно, лучше любо­го из тех, что кроются внутри затемненной области.

Рисунок 4. Построение допустимого и эффективного множества портфелей

 

На рисунке 4 обозначены четыре эффективных портфеля, характеристики которых сведе­ны в таблице 1.5. Портфель А отличается наивысшей ожидаемой доходностью; он цели­ком состоит из инвестиций в акции одной фирмы — Amazon. com. Портфель Г сулит минимальный риск; как легко увидеть из таблицы 1.5, значительную часть в нем зани­мают акции Exxon Mobil, которые имеют самое низкое среднее квадратическое откло­нение. Обратите внимание, что в портфеле Г Boeing и Coca-Cola представлены гораздо меньшими долями, нежели General Motors, хотя акции первых по отдельности сопря­жены примерно с таким же риском. Чем это объясняется? Дело в том, что, как свиде­тельствует прошлый опыт, акции Boeing и Coca-Cola сильно коррелируют с другими акциями из этого портфеля и в силу этого вносят меньший вклад в диверсификацию.

В таблице 1.5 описаны также два других эффективных портфеля — Б и В, для кото­рых характерны промежуточные уровни риска и ожидаемой доходности.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.014 сек.)