АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Акция W Акция М Портфель W, М

Читайте также:
  1. B) Негативная Терапевтическая Реакция.
  2. Bi) Негативная Терапевтическая Реакция как эффект парадокса аналитической медицины.
  3. I. Дифракция Фраунгофера на одной щели и определение ширины щели.
  4. I. Я - Личность, собственная воля, отношение к жизни, реакция на окружающую среду
  5. III. Дифракция Фраунгофера на мелких круглых частицах.
  6. V3: Дифракция света
  7. x.2 Последовательности «воздействие – реакция»
  8. Акция на одну акцию в обращении
  9. Акция «Забота»
  10. Аналитическая химическая реакция
  11. Аналитическая химическая реакция

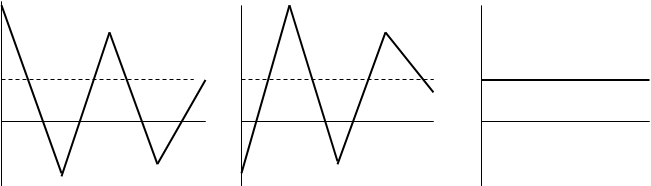
xW, %xM, %xР, %

 

 

25 25

 

15 15 15

 

0 0 0

 

-10 -10 -10

 

 

Рис. 1 Распределение доходности акций W и M, связанных обратной функциональной связью (r = -1.0), и портфеля W, M.

 

Случаем, противоположным функциональной обратной связи (r = -1.0), является прямая функциональная зависимость (r = +1.0). Показатели доход­ности двух акций в этом случае изменяются в одном и том же направлении, а риск портфеля, состоящего из двух таких акций, будет равен риску каждой из этих акций. Таким образом, средние квадратические отклонения порт­феля и его составляющих совпадают, следовательно, диверсификация в этом случае не приводит к снижению риска.действительности большин­ство акций положительно коррелируют друг с другом, но эта связь не является функциональной. Коэффициент корреляции двух случайным образом выбран­ных акций на Нью-Йоркской фондовой бирже составляет около +0.6, а в боль­шинстве случаев r лежит в пределах от +0.5 до +0.7. При таких условиях объединение акций в портфель снижает риск, однако полностью его не элими­нирует.

Мерой риска портфеля может служить по­казатель среднего квадратического отклонения распределения доходности, для расчета которого используется формула (1.6)

(1.8)

где x pi — доходность портфеля, соответствующая i-му состоянию экономики; xp — ожидаемая доходность портфеля; pi — вероятность того, что экономика будет находиться в i-м состоянии.

Эта формула полностью совпадает с формулой расчета среднего квадрати­ческого отклонения отдельного актива (1.3), за исключением того факта, что в данном случае под активом понимается портфель активов.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)