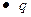АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Градиент

Читайте также:
  1. Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
  2. Выпуклая оптимизация. Условие выпуклости. Субградиентный метод выпуклой оптимизации. Метод растяжения пространства. Метод эллипсоидов.
  3. Градиент потенциала
  4. Градиентные методы
  5. Градиентные методы
  6. Градиентные методы гладкой оптимизации. Общая идея градиентного спуска (подъема). Пропорциональный градиентный метод. Полношаговый градиентный метод. Метод сопряженных градиентов.
  7. Градиентный метод
  8. Градиентный метод в сочетании с методом наискорейшего спуска.
  9. Градиентный метод нелинейного программирования.
  10. Движения внутри поля: от колебания до градиента.
  11. Метод градиента.

Элементы теории поля.

В каждой точке этого пространств V(x, y, z) определена векторная или скалярная функция, тогда говорят, что в пространстве V задано векторное или скалярное поле F(x, y, z, t). F может ещё зависеть и от времени t. Если f

не зависит от t, то поле стационарно:

j=f(x, y, z)

Если заряды с течением времени не меняются, то эти два поля являются стационарными, в простейшем случае Е и F одинаковы во всех точках сферы заданного радиуса окружающих этот заряд.

Градиент

: Пусть в некоторой области задано скалярное поле, выберем

в некотором направлении L две точки М1 и М2, тогда изменение в этом

направлении функции j будет равно:

j = j(М2) -- j(М1).

Расстояние между точками равно dl, тогда производная по направлению от j примет вид:

Т. е. grad скалярной функции, это вектор, модуль которого максимальному значению производной по направлению от этой функции в заданной точке.

Потоком вектора

через поверхность S называют величину равную интегралу от скалярного произведения по поверхности S вектора:

Ф=

Дивергенция:

Дивергенцией векторного поля , через замкнутую поверхность S, называют скалярную величину равную пределу отношения потока вектора через замкнутую поверхность S к объему ограниченному этой поверхностью, при условии что объем стремится к нулю.

Величина div поля в данной точке характеризует наличие источников этого поля, чем больше div в данной точке, тем гуще его силовые линии. Для электростатического поля величина дивергенции определяется величиной заряда, помещённого в данную точку поля.

Суммарный заряд находящийся внутри некоторого объёма V, определяется интегралом:

Поток векторного электрического смещения равен:

Тогда, сравнив две последние формулы, видим:

ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА.

Плотность заряда:
линейная

поверхностная :

обьемная

Z

X

Y

d Ф (AA`BB`) = E (x,y,z) dxdy cos 180 = - E (x,y,z) dxdy

d Ф (DD`CC`) = E (x+dx,y,z)dxdy cos0 = E (x+dx,y,z) dxdy

E (x+dx,y,z) = E (x,y,z) +

d Ф (1-2) = E (x,y,z + ) dxdy - E (x,y,z) dxdy = dxdydz

d Ф (3-4) = dxdydz

d Ф (5-6) = dxdydz

dФ = ( + + ) dxdydz

div a =

: :

ДИВЕРГЕНЦИЕЙ — (расхождение) вектора (а) называют предел отношения потока вектора (а) через замкнутую поверхность к величине объема ограниченного этой поверхностью при условии, что объем стремится к нулю

“ ДИВЕРГЕНЦИЯ “ - это родник в лесу, а поток это количество воды прошедшее через поперечное течение русла реки

- оператор Набла


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.011 сек.)