Основные свойства и модели детерминированного факторного анализа

Как указано выше, различают детерминированный и стохастический виды факторного анализа.

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т.е. результативный показатель может быть представлен в виде произведения, частного от деления или алгебраической суммы показателей, являющихся факторами детерминированной модели. Основные свойства детерминированного подхода к анализу:

• определение детерминированной модели путем логического анализа;

• наличие полной (жесткой) связи между показателями;

• невозможность разделить результаты влияния одновременно действующих факторов, которые не поддаются объединению в одной модели;

• изучение взаимосвязей в краткосрочном периоде. Детерминированный факторный анализ проводится по этапам:

1) построение экономически обоснованной (с позиций факторного анализа) детерминированной факторной модели;

2) выбор приема анализа и подготовка условий для его выполнения;

3) реализация счетных процедур;

4) формулирование выводов.

Таким образом, первоочередная задача факторного анализа состоит в построении модели, которая определяется путем логического анализа.

Детерминированные модели могут быть разного типа:

• аддитивные;

• мультипликативные;

• кратные;

• смешанные.

Аддитивные модели представляют собой алгебраическую сумму показателей и имеют следующую математическую интерпретацию:

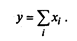
В качестве примера можно привести балансовую модель товарного обеспечения:

где N _p — общий объем реализации; N _зап.I — запасы товаров на начало периода; N _п - объем поступления; N _выб. — прочее выбытие товаров; N _зап.II — запасы товаров на конец анализируемого периода.

Мультипликативная модель представляет собой произведение факторов. В обобщенном виде она может быть представлена формулой:

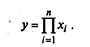
Примером мультипликативной модели является двухфакторная модель объема реализации:

где Ч — среднесписочная численность работников; В — выработка на одного работника.

Кратные модели представляют собой отношение факторов и имеют вид:

где Z — совокупный показатель.

Например,

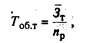
где Т _об.т - срок оборачиваемости товаров (в днях); _т - средний запас товаров; n _р - однодневный объем реализации.

Смешанные модели представляют собой комбинацию перечисленных моделей и могут быть описаны с помощью следующих выражений:

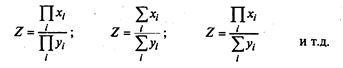
Примером смешанной модели является формула расчета интегрального показателя рентабельности:

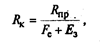
где R _к - рентабельность капитала; R _пр - рентабельность продаж; F _e - фондоемкость основных средств; Е _з - коэффициент закрепления оборотных средств.

Однако не любое математическое выражение может являться факторной моделью. Нельзя путать формулу расчета показателя с моделью, отражающей причинно-следственные связи. Например, выработка как показатель производительности труда рассчитывается делением выручки от реализации на среднесписочную численность работников 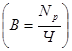, однако это выражение не является моделью, так как не отражает причинно-следственные связи: рост объема реализации не является фактором увеличения производительности труда, равно как и простое сокращение штата не ведет непосредственно к увеличению производительности труда.

Приемы построения детерминированных факторных моделей. В отдельных случаях для изучения зависимости между показателями и количественного измерения множества причин, повлиявших на результативный показатель, следует построить детерминированную факторную модель. Рассмотрим некоторые методы такого построения.

1. Метод удлинения факторной системы.

Исходная факторная модель у=. Если при этом

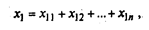
тогда модель примет вид:

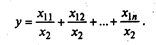
2. Метод расширения факторной системы. При использовании этого метода числитель и знаменатель умножаются на одно и то же число:

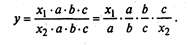
3. Метод сокращения факторной системы. При использовании этого метода числитель и знаменатель делятся на одно и то же число:

где R _к — рентабельность капитала; П — прибыль; S — средняя стоимость основных средств; R _пp — рентабельность продаж; F _е — фондоемкость основных средств.

Детализация, или глубина, факторного анализа во многом определяется числом факторов, влияние которых можно количественно оценить, поэтому большое значение в анализе имеют многофакторные мультипликативные модели (МММ). В основе построения и решения этих моделей лежат следующие принципы:

• место каждого фактора в модели должно соответствовать его роли в формирований результативного показателя;

• модель следует строить из двухфакторной полной модели путем последовательного расчленения факторов, как правило, качественных, на составляющие;

• при написании формулы многофакторной модели факторы рекомендуется располагать в порядке их замены слева направо. Это правило необходимо соблюдать при использовании метода цепной подстановки и его модификаций.

Построение факторной модели — первый этап детерминированного анализа. Далее следует выбрать способ ее решения.

Поиск по сайту: