Оценка риска с использованием вероятностных моделей

Известно, что многие процессы, в том числе и экономические, представляют собой сочетание двух процессов: детерминированного процесса (тренда) и случайного процесса.

Для поиска тренда применяются различные методы: укрупнения интервалов, скользящей средней, гармонического анализа и некоторые другие. Общепринятые способы прогнозирования ситуации на производстве (в промышленности и сельском хозяйстве) и на рынке в основном учитывают только детерминированный фактор. Оценка влияния случайной составляющей процесса на общий результат практически не производится. Это одна из причин того, что прогнозы не всегда оправдываются.

Смоделируем динамику цен на продукцию с учетом развития системы и жизненного цикла товара.

Для того чтобы надлежащим образом сделать прогноз ситуации на производстве и на рынке, необходимо учитывать оба составляющих процесса — и детерминированный, и случайный.

Ситуация на рынке товаров и услуг является определяющей для всей экономической системы страны или региона. От нее зависят финансово-хозяйственное положение предприятий, прибыли торговых и финансовых организаций и вообще всех субъектов хозяйствования.

Для описания положения на рынке можно рассмотреть многомерное пространство, каждый компонент (размерность) которого адекватен некоторому продукту (услуге). Цена данного товара (услуги) на рынке задает координату по данному компоненту многомерного пространства. Тогда конкретная ситуация на рынке в данный момент времени (цены на все товары и услуги, рассматриваемые в математической модели) представляет собой вектор в многомерном пространстве. Начало этого вектора лежит в начале координат, его конец соответствует ценам на товары (услуги) в данный момент времени. Естественно, что с течением времени цены на различные товары и услуги изменяются, следовательно, изменяется и положение вектора в многомерном пространстве. Непрерывная линия, соединяющая концы векторов, соответствующих различным моментам времени, отражает эволюцию ситуации.

На рис. 17.1 схематически изображено изменение экономической ситуации на рынке, которое соответствует некоторой кривой в многомерном пространстве. При этом различные оси (W ₁, W ₂, …, W_n) соответствуют различным товарам, представленным на рынке. Векторы,, — начальный, текущий и конечный векторы — отображают изменение цен на различные товары в разные моменты времени.

Под зависимостью вероятности р от цены х будем понимать тот факт, что в данный момент времени цена на товар будет не больше х. Иногда удобнее работать не с вероятностью некоторого события, а с плотностью вероятностей этого события.

_{i- 1} Плотность вероятностей является производной от вероятности, т.е.

где х - цена на товар; р'(х) - вероятность; ρ (х) - плотность вероятности.

Отсюда вытекает связь между вероятностью и плотностью вероятностей:

Графически связь между плотностью вероятностей и вероятностью проиллюстрирована на рис. 17.2. В качестве примера взят нормальный закон распределения с параметрами: среднее значение равно 2,4, дисперсия — 0,8.

Постановку задачи определения ситуации на рынке товаров и услуг рассмотрим на примере одного продукта. Поскольку эволюция экономической системы представляет собой сочетание двух процессов - один детерминированный, обусловленный объективными причинами, действующими в данной экономической системе, а второй - вероятностный, то для ее описания применяют уравнение Колмогорова, отображающее изменение плотности вероятности в различные моменты времени:

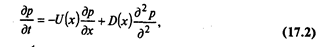
где х - цена на товар; t - время; р - распределение плотности вероятностной цены на товар; U(x) - коэффициент сноса (тренд) - скорость изменения цены на товар; D(x) - коэффициент подвижности -линейная функция дисперсии случайного процесса.

В уравнении (17.2) первое слагаемое описывает детерминированный процесс - тренд, а второе — стохастический процесс. На рис. 17.3 представлено некоторое (произвольное) изменение средней цены на товар во времени.

После некоторых преобразований уравнение (17.2) принимает вид уравнения второй степени в частных производных, которое иногда называется уравнением теплопроводности (диффузии):

где τ и ς — вспомогательные переменные, которые вычисляются в соответствии со следующими уравнениями:

где ς — аналог координаты (цены), τ(t) = D( ς ) + С — аналог времени. Здесь С — постоянная интегрирования, определяемая из начальных условий. Решение уравнения (17.3) выглядит следующим образом:

Поскольку уравнение (17.2) описывает стохастический процесс, то его решение представляет собой распределение плотности вероятностей. Уравнение (17.5) отображает тот факт, что каждой цене на товар ς, в некоторый момент τ соответствует своя плотность вероятности ρ.

На рис. 17.4 представлено распределение плотности вероятностей для некоторого момента времени в зависимости от цены на товар.

Изменение распределения плотности вероятностей в зависимости от условной цены, начиная для некоторого момента времени, представлено на рис. 17.5. Из зависимости между плотностью вероятностей и вероятностью (17.1) вытекает, что для одной и той же цены вероятность будет различной в разные моменты времени.

Решение уравнения Колмогорова (17.5) представляет собой нормальный закон распределения со следующими параметрами: независимая переменная ς с математическим ожиданием равным нулю, дисперсия τ. Из этого уравнения также следует, что с течением времени дисперсия распределения плотности вероятностей увеличивается, т.е. само распределение как бы «расплывается», что можно наблюдать на рис. 17.5. Следовательно, чем больше промежуток времени, на который осуществляется прогноз, тем больше неопределенность полученного результата.

Подставляя в (17.4) x ₀ = 0, а вместо х - закупочную цену на товар, увеличенную на торговые издержки, и решая это уравнение относительно ς, получим оценку критической цены (точки безубыточности) — точка А на рис. 17.6. Принимая во внимание формулы (17.1), (17.5), можно рассчитать вероятность того, что цена на товар будет меньше или равна цене приобретения, увеличенной на торговые издержки в соответствии с формулой, показывающей риск продавца:

где С* — сумма закупочной цены на товар и торговых издержек.

Следовательно, различным прогнозируемым ситуациям на рынке соответствуют различные вероятности. Отсюда также вытекает, что прогноз экономического положения различных субъектов хозяйствования является величиной вероятностной.

Расчет риска продавца. Как уже сказано выше, риск продавца заключается в том, что отпускная цена на товар окажется ниже закупочной. Для расчета этого риска необходимо определить зависимость вероятности от отпускной цены на товар, для чего следует вычислить интеграл (17.6).

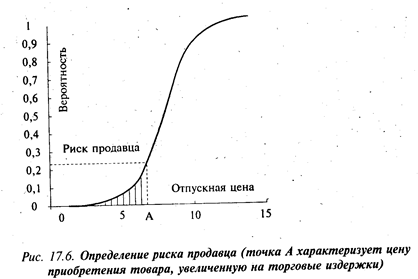
Используя рис. 17.6 для различных моментов времени, можно рассчитать зависимость риска, т. е. вероятности того, что доход от продажи товара не компенсирует затрат на его покупку и хранение, от времени — заштрихованный участок на рисунке. В этом случае продавец, ориентируясь на изменение риска во времени и учитывая то, что при длительном хранении растут расходы и происходит омертвление капитала, сам вправе выбирать момент продажи своего товара.

Оценка риска производителя. Для оценки риска производителя удобно использовать калькуляцию себестоимости производства продукции. В калькуляции указаны основные статьи расходов: затраты на материалы, заработную плату, отчисления в бюджет и внебюджетные фонды и т.д. По каждой из калькуляционных статей расходов можно написать уравнение (17.2) и найти его решение (17.3), т. е. определить изменение распределения вероятностей с течением времени. Таким образом, для каждой статьи расходов в калькуляции себестоимости существует свое распределение с соответствующими средними значениями и дисперсией распределения. Поскольку себестоимость производства той или иной продукции определяется как сумма статей расходов, то общее математическое ожидание распределения себестоимости будет равно сумме средних значений слагаемых — статей расходов, а дисперсия себестоимости — сумме дисперсий статей расходов.

Цена на производимый продукт также рассчитывается с помощью уравнения (17.2), для которого находится решение (17.5). В результате имеются два распределения: плотности вероятности себестоимости и плотности вероятности цены на производимый продукт. Риск производителя будет заключаться в определении вероятности того, что полученная прибыль окажется меньше запланированной, т.е. себестоимость окажется равной цене товара или превышающей ее. В этом случае производитель товара будет нести убытки от своей деятельности. Для того чтобы рассчитать вероятность риска, необходимо рассчитать условную вероятность того, что цена будет иметь определенное значение при условии, что полученная прибыль принимает другое значение. Эта вероятность рассчитывается по формуле условной вероятности для зависимых событий:

где Р(А| В) — вероятность того, что цена будет иметь некоторое значение при условии, что полученная прибыль имеет другое значение; Р(АВ) — вероятность того, что и цена, и полученная прибыль будут иметь одинаковое значение; Р(А) — вероятность того, что цена будет иметь определенное значение.

В этом случае критическая цена (С *), равная себестоимости производимого продукта, увеличенной на торговые издержки, находится способом, аналогичным нахождению критической цены при расчете риска продавца (см. выше). А при расчете риска предпринимателя в качестве подынтегральной функции в (17.6) берется распределение, рассчитанное по формуле условной вероятности. Таким образом, риск предпринимателя, который занимается производством и реализацией продукции, складывается из риска получить высокую себестоимость производимого продукта и низкую цену при его реализации.

Риск инвестора (финансовый риск). Наиболее сложно рассчитывать риск инвестора. При инвестировании финансовых средств в некоторый проект необходимо учитывать большое количество факторов, которые могут оказывать влияние на окончательный результат проекта. Это могут быть проектно-конструкторские разработки, строительно-монтажные работы, ввод в действие производственных мощностей, в которые инвестируются денежные средства, и многое другое. Основное отличие риска инвестора от риска производителя заключается в том, что отдача, получение прибыли на вложенный капитал значительно растянуты во времени (временной лаг). Чтобы определить риск инвестора, необходимо учитывать, помимо всех остальных статей расходов (см. выше), еще и временной фактор. Поэтому для оценки риска инвестора необходимо рассчитать риск производителя в каждый момент времени (имеется в виду прогнозирование риска). Затем рассчитывают среднее значение риска в любой момент времени по формуле:

где R — средний риск инвестора; Т — горизонт прогнозирования; r(t) — риск производителя в момент времени t.

Применение данной методики позволяет получить численные значения коммерческого риска, риска производителя и инвестора. Полученные данные имеют вероятностный характер и служат основой для принятия управленческих решений по рассматриваемому проекту.

Резюме

Поиск по сайту: