Лекція № 2. Пряма. Взаємне положення двох прямих

План лекції

1. Положення прямої відносно площин проекцій.

2. Сліди прямої.

3. Визначення натуральної величини та кутів нахилу прямої до площин проекцій.

4. Пропорційний поділ відрізку прямої.

5. Належність точки прямій.

1. Положення прямої відносно площин проекцій. Положення прямої відносно площин проекцій вважають визначеним, якщо відомі проекції двох точок цієї прямої. Відносно площин проекцій П1, П2, П3 пряма може займати 7 положень.

Пряма загального положення (рис. 2.1) розташована під довільними кутами нахилу до площин проекцій.

Рис. 2.1

А1В1; А2В2; А3В3 x; y; z.

Прямі рівня – паралельні до однієї з площин проекцій, тому на цю площину вони проектуються в натуральну величину.

А) Горизонталь h║П1 (рис. 2.2).

Для визначення положення прямої достатньо аналізу двох її проекцій П1 і П2.

h2║x

h1- HB Рис. 2.2

─────

h║П1

Б) Фронталь f║П2 (рис. 2.3).

f1║x

f2- HB

─────

f║П2 Рис. 2.3

B) Профільна пряма рівня р║П3 (рис. 2.4).

I) p2║Z

p2┴x

II) p1║у

p1┴x

III) p3 - нв

─────

р║П3

Рис. 2.4

Проекціюючі прямі перпендикулярні до однієї з площин проекцій, тому на цю площину проектуються у вигляді точки. До двох інших площин такі прямі паралельні.

А) Горизонтально-проектуюча пряма L┴П1 (рис. 2.5).

L2┴x

─────

L┴ П1 Рис. 2.5

Б) Фронтально-проектуюча пряма АВ┴П2 (рис. 2.6)

А1В1┴x

─────

АВ┴ П2

В) Профільно-проектуюча пряма m ┴ П3 (Рис. 2.7). Рис. 2.6

I) m2║x

m2┴z

II) m1║x

m1┴y

─────

m┴П3

Рис. 2.7

2. Сліди прямої. Сліди прямої – це точка перетину заданої прямої з площиною проекції. Побудування слідів прямої розглянемо на конкретному прикладі.

Приклад: Побудувати слід відрізку прямої АВ.

А) Для побудування горизонтального сліду прямої необхідно Н:

1) Продовжити фронтальну проекцію прямої до перетину з віссю х.

2) З точки перетину опустити перпендикуляр до перетину з продовженням горизонтальної проекції прямої (рис. 2.8).

Слід прямої завжди належить до площини прямої і тому співпадає зі своєю проекцією на цю площину.

Недостатня проекція сліду завжди буде розташована на вісі проекції х.

I) A2B2∩x=H2

II) H2H1∩ A1B1=H

III) H є П1

Н≡Н₁, Н₂ є х Рис. 2.8

Б)Для побудування фронтального сліду F необхідно:

1) Продовжити горизонтальну проекцію прямої до перетину з віссю х.

2)З точки перетину підняти перпендикуляр до перетину з продовженням фронтальної проекції прямої (рис. 2.8).

I) A₁B₁×X=F₁

II) F₁F₂× A₂B₂=F₁

III) Fє П2, F≡F₂

F₁ є х

Рис. 2.9

3. Визначення натуральної величини та кутів нахилу прямої до площин проекцій. Рішення цієї задачі виконують на основі методу прямокутного трикутника.

Приклад:

Визначити натуральну величину та кути нахилу до П1, П2.

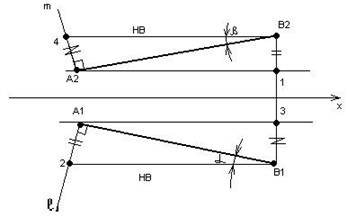Рішення задачі на П1 у наступній послідовності:

I) A₂1║x

II) L є A1

L┴A₁B₁

III) B₂1=A₁2

B₁2 – HB

α – кут нахилу прямої в просторі до П1

Для визначення натуральної величини та кута нахилу прямої до П2 необхідно виконати аналогічні побудови на П2. Рис. 2.10

I) A₁3║x

II) m┴A₂B₂

III) B₁3=A₂4

IV) B₂4 – HB

V) β

β – кут нахилу прямої до П2 (рис. 2.10).

2.4. Пропорційний поділ відрізку прямої. Рішення цієї задачі виконують з використанням допоміжної прямої.

Приклад:

Відрізок АВ поділити у співвідношенні 2:3 (рис. 2.11).

Послідовність рішення:

1) Через А₁ будуємо довільну пряму L під довільним гострим кутом до А₁В₁.

L є А₁

2) 2+3=5. Визначаємо кількість відрізків поділу

3) Від А відкладаємо п’ять довільних, але рівних між собою відрізків на L.

4) А₁1=12=23=34=45

5) 5 з’єднуємо з В₁ – отримуємо 5В₁.

6) С₁2║ 5В₁

7) С₂ є А₂В₂

8) А₂С₂ = А₁С₁ = 2

В₂С₂ В₁С₁ 3. Рис. 2.11

5. Належність точки до прямої. Точка належить до прямої, якщо її проекції розташовані на відповідних проекціях прямої.

I) A₂ ¢ m₂

II) A₁ є m₁

─────

A ¢ m (рис. 2.12)

Рис. 2.12

I) A₂ є h₂

II) A₁ є h₁

─────

A є h (рис. 2.13)

Рис. 2.13

Послідовність рішення задач з нарисної геометрії:

1) Аналізуємо графічні умови задачі та з’ясовуємо властивості геометричних образів.

2) Визначаємо алгоритм рішення задачі.

3) Розв’язуємо задачу.

Контрольні питання

1. Скільки положень може займати пряма лінія відносно площин проекцій?

2. Як розташовані проекції фронталі та горизонталі відносно вісі ХY?

3. Що називається слідом прямої?

4. Як побудувати горизонтальний та фронтальний сліди прямої?

5. Яким методом визначають натуральну величину та кути нахилу прямої до площин проекцій?

6. Сформулюйте умову належності точки до прямої.

Поиск по сайту: