Лекція № 6. Перетин двох площин, прямої та площини

План лекції

1. Перетин двох площин:

а) одна з яких – площина окремого положення;

б) обидві площини загального положення;

в) визначення елементів видимості;

г) площин заданих слідами.

2. Перетин прямої та площини;

а) площина задана плоскою фігурою, паралельними або пересічними прямими;

б) площина задана слідами;

в) визначення елементів видимості.

1. Взаємний перетин двох площин. Результатом перетину двох площин є пряма лінія. Для побудування її проекцій необхідно визначити дві точки, які одночасно належать до двох площин.

Рішення кожної конкретної задачі залежить від графічних умов, якими

задають площини на кресленні.

В більшості випадків необхідно використовувати допоміжні площини окремого положення, що значно спрощує рішення задач.

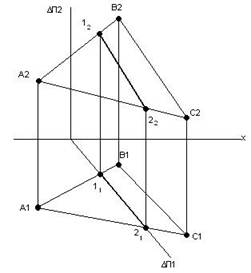
Приклад 1 (рис. 6.1). Побудувати лінію перетину двох площин Г×∆=KL.

Оскільки ∆┴П1, горизонтальний слід цієї

прямої має збиральні властивості.

Рис. 6.1

Горизонтальна проекція прямої буде розташована на ∆П1.

1. ∆П₁×А₁В₁=1₁

∆П₁×А₁С₁=2₁

2. 1₂ є А₂В₂

2₂ є А₂С₂

──────────

Г×∆=1,2

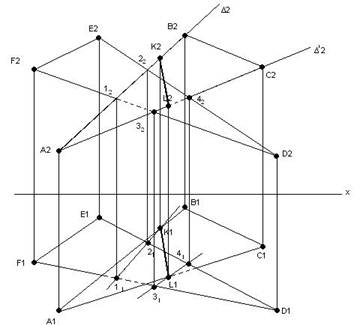
Приклад 2 (рис. 6.2): Побудувати лінію перетину площин загального положення, які задані плоскими геометричними фігурами.

Для рішення цієї задачі необхідно використати допоміжні проектуючі площини, які дадуть змогу отримати рішення задачі.

1.AB є ∆; ∆┴П₂

∆₂×D₂F₂=1₂

∆₂×D₂E₂=2₂

1₁ є D₁F₁

2₁ є D₁E₁

1₁2₁×A₁B₁=K₁

K₂ є A₂B₂

2. AC є ∆’; ∆’┴П₂

∆’₂ ×D₂F₂=3₂

∆’₂ ×D₂E₂=4₂

3₁ є D₁F₁

4₁ є D₁E₁

3₁4₁×A₁C₁=L₁

L₂ є A₂C₂

Рис. 6.2 K₁L₁; K₂L_2.

Лінія перетину двох площин ділить кожну площину на 2 частини – видиму і невидиму.

Для визначення елементів видимості пересічних площин необхідно використати рішення аналогічної задачі для мимобіжних прямих.

Якщо пересічні площини задані слідами, то лінію перетину будують у наступній послідовності:

1) позначають точки перетину однойменних слідів;

2) будують недостатні проекції цих точок, які завжди будуть розташовані на вісі х;

3) з’єднують однойменні проекції точок.

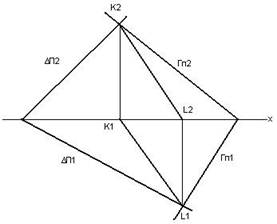Приклад. Побудувати лінію перетину двох площин ∆ і Г.

∆ × Г=KL

Площини ∆ і Г – площини загального положення, а тому і лінія їх перетину – пряма загального положення.

Рішення задачі виконують

Рис. 6.3 відповідно до загального алгоритму.

1. ∆П2 × Гп2=K2

∆П1 × Гп1=L1

2. K1, L1 є x

3. K2L2; K1L1 (рис. 6.3).

Якщо одна з площин займає окреме положення, то побудування лінії перетину має певні особливості.

Приклад 1. Побудувати лінію перетину двох площин ∑×∆=KL

∆┴П₁, тому горизонтальна проекція лінії перетину K₁L₁ буде належати до ∆_П1.

1. ∑_П2×∆_П2=K₂

∑_П1×∆_П1=L₁

2. K₁L₁ є ∆_П1

3. L₂ є x; K₂L₂ (рис. 6.4).

Рис. 6.4

Приклад 2. Побудувати лінію перетину двох площин Г×Θ.

1. Θ║П₁, Θ┴П₂, а тому на П₂ l є Θ₂

2. Г_П2×l₂=1₂

3. l₁║Г_П1 (рис. 6.5).

2. Перетин прямої та площини. Результатом перетину прямої та площини є

Рис. 6.5 точка.

Для побудування її проекцій необхідно:

1) Пряму заключити у допоміжну площину(проекціюючу або рівня).

2) Побудувати лінію перетину прямої та заданої площин

3) Позначити точку перетину лінії перетину двох площин та заданої прямої.

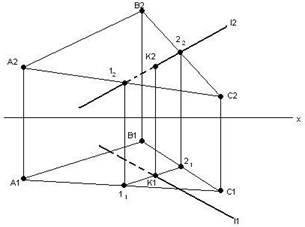Приклад. Побудувати точку перетину прямої та площини.

1. l є ∑; ∑┴П₂

2. ∑₂×Г(ABC)=1,2

∑₂×A₂C₂=1₂

∑₂×B₂C₂=2₂

3. 1₁ є A₁C₁

2₁ є B₁C₁

4. 1₁2₁×l₁=K₁

5. K₂ є l₂ (рис. 6.6).

Рис. 6.6

Контрольні питання.

1. Як побудувати лінію перетину двох площин, заданих плоскими геометричними фігурами?

2. Як побудувати лінію перетину двох площин, заданих слідами?

3. Як побудувати точку перетину прямої та площини?

4. Як визначити елементи видимості пересічних площин, прямої та площини?

Поиск по сайту: