Лекція № 10. Перетин поверхні площиною. Перетин прямої та поверхні

План лекції

1. Перетин гарних поверхонь площиною.

2. Перетин поверхонь обертання площиною.

3. Перетин прямої та поверхні.

1. Перетин граних поверхонь площиною. Результатом перетину граної поверхні з площиною є замкнута ламана лінія. Для побудування точок цієї лінії використовують допоміжні січні площини або інші методи в залежності від конкретних умов задачі. Головним елементом рішення задач є визначення точок, які одночасно належать до січної площини та геометричної поверхні.

Приклад 1. Побудувати лінію перетину призми площиною Г.

Г – площина загального положення.

Призма розташована на П1.

Її бокові грані – горизонтально-проектуючі площини, а ребра – горизонтально-проектуючі прямі, які мають на П1 збиральні властивості, а тому горизонтальна проекція лінії перетину співпадає з проекцією

Рис. 10.1 призми на П1.

1.A₁≡1₁; B₁≡2₁; C₁≡3₁; D₁≡4₁.

Подальше рішення задачі зводиться до побудування фронтальних проекцій точок 1,2,3,4, які одночасно належать до призми і площини Г. Для цього використовуємо фронталі площини Г.

2.f₂^/×A₂E₂=1₂

3.f₂×B₂M₂=2₂

4.f₂^///×C₂N₂=3₂

5.f₂^//×D₂K₂=4₂

На П2 з’єднуємо 1₂, 2₂, 3₂, 4₂ відрізками прямих, враховуючи те, що 2₂ є невидима.

1₂3₂,3₂4₂ – видимі;

1₂2₂, 2₂4₂ – невидимі (рис. 10.1).

Приклад 2. Побудувати лінію перетину піраміди з площиною ∑ та визначити натуральну величину перерізу (рис. 10.2).

Аналіз графічних умов:

- ∑ - фронтально-проектуюча площина, а тому ∑п2 має збиральні властивості;

- у зв’язку з цим позначаємо точки перетину ∑п2 з боковими ребрами піраміди;

- натуральну величину визначаємо методом заміни площин проекцій.

1. ∑п₂×S₂A₂=1₂

∑п₂×S₂B₂=2₂

∑п₂×S₂C₂=3₂

2. 1₁ є S₁A₁

2₁ є S₁B₁

3₁ є S₁C₁

3. П₁→П₄

х_2.4║1₂2₂3₂

Рис. 10.2 ∆1₄2₄3₄ – НВ.

2. Перетин поверхонь обертання площиною. В результаті перетину поверхонь обертання площиною утворюється замкнута крива лінія. Загальна послідовність у розв’язанні задачі полягає у наступній послідовності дій:

1) використовуємо допоміжні січні площини окремого положення;

2) будуємо лінію перетину заданої поверхні з допоміжною січною площиною;

3) будуємо лінію перетину допоміжної і заданої площин;

4) позначаємо точки перетину лінії перетину поверхні з допоміжною площиною з лінією перетину площин.

Приклад: Побудувати лінію перетину конусу з площиною ∑ (рис. 10.3).

План рішення:

1) будуємо проекції крайньої верхньої та нижньої точок перетину, використовуючи допоміжну горизонтально-проектуючу площину Г.

1. Г┴П₁

2. Г₁┴∑п₁

Г₁ є S₁

3. Г₁×K₁=1₁2₁

4. Г×∑=3,4

5. 3₂4₂×S₂2₂=A₂

3₂4₂× S₂1₂=B₂

6. A₁B₁ є Гп₁

2) будуємо проекції крайньої правої та лівої точок лінії перетину, для цього використовуємо допоміжну січну площину ∆║П₂.

7. ∆║П₂

∆П₁║х

∆П₁ є S₁

8. ∆×∑= f

f₂×S₂5₂=C₂

f₂×S₂6₂=D₂

C₁D₁ є ∆П₁

9. Θ║ П₁

Θ×K= R

10. Θ×∑=h

h₁×R₁=E₁, F₁

E₂, F₂ є Θ₂

Рис. 10.3

На П1 лінія перетину – видима замкнута крива

На П2 лінія перетину має дві частини:видиму і невидиму.

Межові точки видимості – крайня права і ліва точки (С2, D2)

А2, Е2 – видимі

С2, D2, B2, F2 – невидимі.

3. Перетин прямої та поверхні. В результаті перетину прямої та поверхні утворюються дві точки: входу та виходу.

Для побудування їх проекцій необхідно:

1) пряму заключити у допоміжну січну площину окремого положення;

2) побудувати лінію перетину поверхні з допоміжною площиною;

3) позначити точки перетину заданої прямої з лінією перетину поверхні площиною;

4) визначити видимість прямої, яка на інтервалі точок входу-виходу невидима.

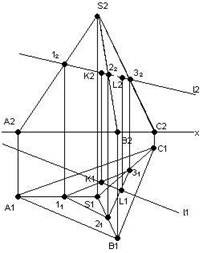
Приклад 1. Побудувати точки перетину прямої l та піраміди (рис. 10.4).

1. l є Г

Г┴П₂

2. 1₂2₂3₂ є Г₂

3. 1₁ є S₁A₁

2₁ є S₁B₁

3₁ є S₁C₁

4. l₁×1₁3₁=K₁

l₁×2₁3₁=L₁

K₂, L₂ є Г₂ Рис. 10.4

Деякі задачі вирішують за допомогою методу заміни площин проекцій.

Приклад 2. Побудувати точки перетину прямої l та сфери (рис. 10.5).

1. П₁/П₂→П₁/П₄

х_1.4║А₁В₁

K₄L₄

2. K₁L₁; K₂L₂.

Рис. 10.5

Контрольні питання.

1. Які геометричні образи є результатом перетину граних поверхонь та поверхонь обертання площиною?

2. Наведіть приклади рішення задач.

3. Сформулюйте послідовність рішення задачі по визначенню точки перетину прямої та поверхні.

Поиск по сайту: