Лекція № 3. Взаємне положення двох прямих

План лекції

1. Паралельність двох прямих.

2. Перетинні прямі.

3. Мимобіжні прямі.

4. Взаємноперпендикулярні прямі (одна із них – пряма рівня).

5. Теорема про проекіювання прямого кута.

1. Паралельні прямі. Дві прямі паралельні, якщо їх проекції на П1, П2, П3 також паралельні. Для прямих загального положення достатньо паралельності проекцій на двох площинах П1 та П2.

Рішення задач з цього розділу поділяються на дві групи:

1) Побудування прямої, паралельної до заданої

2) Перевірка паралельності двох прямих.

Рішення обох задач розглянемо на конкретних прикладах.

Приклад 1:

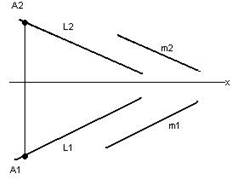
Через точку А побудувати L║m.

L є m

L ║ m

────

Дамо загальну схему рішення будь-якої геометричної задачі:

Рис. 3.1

I) Аналізуємо графічні умови задачі (з’ясовуємо основні властивості проекцій геометричних образів, а також їх положення відносно площин проекцій)

II) Визначаємо послідовність побудування, а також ту площину проекцій, на якій починають виконувати побудування.

Рішення:

1. L2 є A2

L2║m2

2. L1 є A1

L1║m1

────

L║m

(рис. 2.11)

Приклад2:

Перевірити паралельність прямих AB та CD.

A₃B₃╫C₃D₃

AB╫CD (рис. 3.2). Рис. 3.2

2. Перетинні прямі. У перетинних прямих проекції також перетинаються і крім того, проекції точки перетину знаходяться на одній лінії проекційного зв’язку, бо точка перетину одночасно належить відразу Рис. 3.3

до двох прямих і є їх спільною точкою.

Рішення типових задач цього розділу розглянемо на конкретних прикладах.

Приклад 1:

Через точку А побудувати пряму L, пересічну до m:

A, m

1. L₂ є А₂

L₂∩m₂=K₂ Рис. 3.4

2. K₁ є m₁

3. A₁K₁ – L₁∩m₁

─────────

L∩m=K (рис. 3.4)

Приклад 2:

Визначити взаємне положення двох прямих АB та СD.

1. A₃B₃∩C₃D₃=K₃

2. A₂B₂∩C₂D₂≠K₂

3. A₁B₁∩C₁D₁=K₁

─────────

CD AB (рис. 3.5)

Приклад 3:

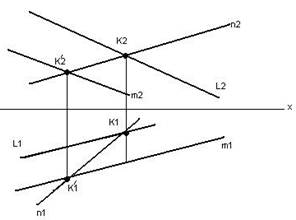
Прямі L, m перетнути прямою n.

1. n₂∩L₂=K₂

n₂∩m₂=K^/₂

2. K₁ є L₁

K^/₁ є m₁

3. K₁ K^/₁ - n₁

───────

Рис. 3.5 n×L=K, n×m=K^/ (рис. 3.5)

3. Мимобіжні прямі. У мимобіжних прямих проекції пересічні, але проекції точки перетину не розташовані на одній лінії проекційного зв’язку, бо мимобіжні прямі не перетинні і не мають спільної точки. Точка перетину проекцій мимобіжних прямих – це в дійсності дві точки, які належать до різних прямих.

L • m

В цьому випадку виникає задача по визначенню видимості конкуруючих

Рис. 3.6 точок (рис. 3.6).

На П1 буде видима точка, фронтальна проекція якої розташована вище відносно вісі х.

Проекції розташовані довільно. На П2 буде видима точка, горизонтальна проекція якої розташована нижче відносно вісі х.

4. Взаємно-перпендикулярні прямі (одна з прямих – пряма рівня). Рішення цієї задачі починають на тій площині проекцій, до якої паралельна задана пряма, бо на цій площині ми маємо натуральну величину прямої, а також її натуральне положення відносно осей проекцій.

Приклад:

Через точку А побудувати пряму L┴ до n.

L є A, L┴ n

1. L₁ є A₁

L₁×n₁=K₁

2. K₂ є n₂ Рис. 3.7

3. K₂A₂ – L₂ (рис. 3.7)

5. Теорема про проекціювання прямого кута. Прямий кут проекціюється в натуральну величину, якщо хоч одна з його сторін паралельна до цієї площини проекцій.

1. <ABC=90°

2. AB║П1

AB║ A₁B₁; BC╫П1

─────────

<A₁B₁C₁=90°

─────────

1. AB┴BC

2. AB┴BB₁(на основі ортогонального методу проекціювання) Рис. 3.8

3. BB₁×BC - ∑

4. B₁C₁ є ∑

5. AB┴∑

6. AB║ A₁B₁

7. A₁B₁┴∑

8. Так як B₁C₁ є ∑, то A₁B₁┴ B₁C₁

─────────

<A₁B₁C₁=90° (рис. 3.8)

Контрольні питання

1. Як розташовані проекції паралельних прямих?

2. Як розташовані проекції пересічних та мимобіжних прямих?

3. Як визначають видимість конкуруючих точок на П₁ та П₂?

4. Сформулюйте теорему про проекціювання прямого кута.

Лекція № 4. Площина

План лекції

1. Завдання площини на кресленні.

2. Сліди площини.

3. Положення площини відносно площин проекцій.

Рис. 4.1 4. Головні лінії площини.

5. Належність прямої та точки до площини.

1. Завдання площини на кресленні. В нарисній геометрії площину представляють як результат послідовного переміщення однієї прямої вздовж іншої. Площина взагалі необмежена, тому на кресленні її

Рис. 4.2 задають слідуючими геометричними елементами:

1) Трьома точками, що не належать одній прямій - Г(А,В,С) (рис. 4.1).

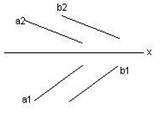
2) Прямою і точкою, яка не належить прямій - А ¢ l, ∆(l, A) (рис. 4.2).

Рис. 4.3 3) Паралельними прямими - ∑(а║b) (рис. 4.3).

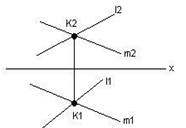4) Пересічними прямими - R(l×m) (рис. 4.4).

5) Плоскою геометричною фігурою - Θ(∆АВС) (рис. 4.5).

Але найбільш поширеним методом завдання площин є завдання слідами.

Рис. 4.4 3.2. Сліди площини

Слід площини – це лінія перетину заданої площини з площиною проекцій (рис. 4.6).

∑п₁ – горизонтальний.

∑п₂ – фронтальний.

∑п₃ – профільний сліди площин.

∑x, ∑y, ∑z – точки сходу слідів.

Рис. 4.5

3. Положення площини відносно площин проекцій. Відносно площин проекцій будь-яка площина може займати 7 положень.

1) Площина загального положення (рис. 4.6)

Розташована під довільними кутами нахилу до П1, П2, П3. На площинному кресленні сліди цієї площини розташовані під довільними

Рис. 4.6

кутами нахилу до осей проекції (рис 4.6).

2) Площини рівня.

Паралельні до однієї з площин проекцій і одночасно перпендикулярні до двох інших.

А) Горизонтальна площина рівня – паралельна до П1 (рис. 4.7).

1. ΘП2║х

───── Рис. 4.7

2. Θ║ П₁

А₂, В₂, С₂ є Θ

А₁, В₁, С₁ – нв.

Б) Фронтальна площина рівня (паралельна до П2). Рис. 4.8

∑п₁║х

─────

∑║П₁ (рис. 4.8).

В) Профільна площина рівня (паралельна до П3).

1. Гп₂║z

Гп₂┴х

2. Гп₁║у

Гп₁┴х

─────

Г║П₃

Проекції будь-якого геометричного образу, який належить до площини рівня, на одній площині проекцій будуть розташовані на сліді площини (DА₂В₂С₂ÎQ_П2), а на іншу площину Рис. 4.9

геометричний образ проектується в натуральну величину (рис. 4.7).

3) Проекціюючі площини (перпендикулярні до однієї з площин проекцій і непаралельні до інших).

А) Горизонтально-проектуюча площина - перпендикулярна до П1 (рис. 4.10).

1. ∆_П2┴х

─────

∆┴ П₁

1. ∆АВС є ∆

2. ∆А₁В₁С₁ є ∆_П1

Рис. 4.10

Якщо в проекціюючій площині розташовано будь-який геометричний образ, то його проекція завжди буде належати до сліду площини на тій площині проекції, до якої перпендикулярна задана площина. Ця властивість сліду називається збиральною.

Рис.4.11 Рис. 4.12

Б) Фронтально-проектуюча площина - перпендикулярна до П2 (рис. 4.11).

∑п₁┴х

───── (рис. 4.11).

∑┴П₂

В) Профільно-проектуюча площина - перпендикулярна до П3 (рис. 4.12).

1. Гп₂║х

Гп₂┴z

2. Гп₁║х

Гп₁┴у

─────

Г┴П₃

3.4. Головні лінії площини. До головних ліній площини відносять фронталь, горизонталь та лінію найбільшого схилу площини.

Фронталь – пряма, що належить до площини і паралельна до П2.

F є Г

Побудову фронталі починаємо на тій площині проекцій, на якій відоме її положення відносно вісі х.

1. f1║x

f1×Гп1=11

2. 1₂ є х

3. f₂║Гп₂

─────

Рис. 4.13 f є Г (рис. 4.13).

Горизонталь – це пряма, що належить до площини і паралельна до П1.

h₂║x

1. h₂×∆п2=12

2. 11 є х

3. h₁║∆п1

─────

h є ∆

Фронталь та горизонталь площини широко

Рис. 4.14 використовують при рішенні задач по визначенню недостатніх проекцій точок, що належать до площини.

Лінія найбільшого схилу – це пряма, що належить до площини і перпендикулярна до горизонталі площини.

Приклад: Побудувати лінію найбільшого схилу через вершину В.

1. h₂║x

2. h₂×B₂C₂=1₂

3. 1₁ є B₁C₁

4. A₁1₁ – h₁

5. l₁┴h₁

6. l₁×A₁C₁=2₁

7. 2₂ є A₂C₂

8. B₂2₂ – l₂ (рис. 4.15).

3.5. Належність прямої та точки до площини. Пряма належить до площини, якщо:

1) вона проходить через дві точки цієї площини;

2) через одну точку площини і паралельна до Рис. 4.15

іншої прямої площини або до однієї з площин проекцій.

Приклад: В площині ∑ побудувати АВ.

1.А₂ є ∑п₂

А₁ є х

2.В₁ є ∑п₁

В₂ є х

3.С₁ є А₁В₁

С₂ є А₂В₂

─────

С є ∑ (рис. 4.16).

Рис. 4.16 Звідси виходить нова умова належності прямої до площини.

3) Пряма належить до площини, якщо її сліди розташовані на відповідних слідах цієї площини.

Точка належить до площини, якщо вона належить до прямої цієї площини.

Рішення задач складається з двох етапів:

1) Будують пряму, яка належить до площини (рис.4.16)

2) На прямій АВ будують т.С. яка і буде належати до площини.

Контрольні питання.

1. Якими геометричними образами задають площину на кресленні?

2. Що називається слідом площини?

3. Скільки положень і які саме може займати площина відносно площин проекцій?

4. Назвіть положення проекцій фронталі та горизонталі площини відносно до її слідів.

5. Сформулюйте умови належності прямої та точки до площини.

Поиск по сайту: