Метод обертання навколо головних ліній креслення (фронталі і горизонталі)

Цей спосіб використовується. Якщо необхідно сумістити геометричний образ з площиною рівня.

В процесі переміщення кожна точка рухається у відповідних проекціюючих площинах.

Для рішення задачі необхідно визначити:

1) Центр обертання

2) Радіус обертання

Приклад 1: Побудувати нову проекцію точки А методом обертання навколо горизонталі. (Рис. 8.5).

1.∑п₁┴h₁

∑п₁ є A₁

∑п₁×h₁=O₁

O₂ є h₂

2. A₂1=A₁2

O₁2 – HB R

3. A₁^/ є ∑п₁

Рис. 8.5

Приклад 2: Методом обертання навколо горизонталі визначити натуральну величину ∆АВС (Рис.

1. ∑ є В

∑ ┴ h

∑п₁×h1=O₁

O₂ є h₂

2. O₁2 – R

B^/₁ є ∑п₁

3. Гп₁ є С₁

Гп₁┴ h₁

4. Гп₁×В₁^/1₁=С₁^/

5. А₁В₁^/С₁^/ - НВ

Рис. 8.6

Обертання навколо фронталі

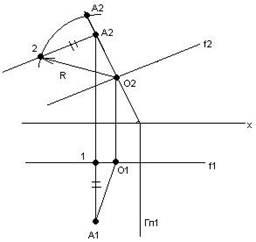Приклад 3: Побудувати нове положення т. А методом обертання навколо фронталі. (Рис. 8.7)

А,f

1.Гп₂┴f₂

Гп₂×f₂=O₂

O₁ є f₁

A₁1=A₂2

O₂2 – HB R

A₂^/ є Гп₂

Рис. 8.7

Поиск по сайту: