Министерство образования и науки Российской Федерации 2 страница

. (6.8)

Як відомо з дисципліни ТАУ, КЧХ реального П-регулятора визначається з його передатної функції шляхом заміни в ній оператора Лапласа s на jω і запису КЧХ або в декартовій системі координат у вигляді суми дійсної Re _Р^П(ω) та уявної Im _Р^П(ω) складових, або в радіальній системі координат у вигляді модуля (довжини) M_Р^П(ω) та з аргумента (кута повороту) θ_Р^П(ω) вектора годографа:

,

де

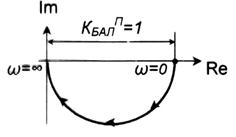
КЧХ ідеальної П-ланки зображується у вигляді точки на відстані К_Р на дійсній осі графіка КЧХ (рисунок 3.8,а) для всього діапазону частот вхідного сигналу –∞ < ω < +∞:

КЧХ інерційної ланки першого порядку (баластної ланки реального П-регулятора) зображена на рисунку 6.8,б. При ω = 0 її годограф починається на дійсній осі графіка КЧХ в точці з одиничним значенням коефіцієнта передачі, а із збільшенням частоти вхідного сигналу ω → ∞ модуль її вектора M_Р^П (коефіцієнт передачі ланки) зменшується від початкового значення до нуля, її аргумент θ_Р^П (кут зміщення між фазами вхідного і вихідного сигналів) збільшується від 0 до 90º. Форма годографа – півколо.

.

.

а) б)

Рисунок 6.8 – КЧХ складових реального П-регулятора

а – ідеального П-регулятора, б – баластної ланки

На рисунку 6.9,а зображена КЧХ реального П-регулятора, що представляє собою промасштабовану в K_P раз КЧХ баластної ланки. По КЧХ можна знайти граничне значення частоти вхідного сигналу, при якій виконуються умови (6.8) роботи П-регулятора в ОНР. При дозволених значення частоти вхідного сигналу ОНР П-регулятора цілком визначається параметром налаштування П-регулятора K_P (рисунок 6.9,б).

а) б)

Рисунок 6.9 – КЧХ (а) та ОНР (б) реального П-регулятора

б) без охоплення ВМ постійної швидкості зворотним зв’язком

Оскільки виконавчий механізм в цьому випадку не охоплюється зворотним зв’язком, то П-регулятор побудований по комбіноваму методу корекції: перша частина регулятора (КПП) побудована за методом паралельної корекції, тобто використовує властивості граничної системи, а ВМ постійної швидкості включений послідовно з нею (рисунок 6.10).

Рисунок 6.10 – Структурна схема П-регулятора за варіантом б)

Проаналізуємо властивості такого П-регулятора за стандартною схемою:

1. Визначимо передатну функцію ланки зворотного зв’язку для формування даною структурою П-закону регулювання, для чого запишемо еквівалентну передатну функцію з’єднання ланок за схемою, зображеною на рисунку 6.8, і прирівняємо її до передатної функції ідеального П-регулятора:

,

Поділимо чисельник і знаменник виразу на K ₁:

.

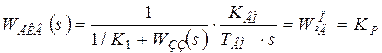Враховуючи, що в граничній системі при K ₁→∞ вiдношення 1/ K ₁→0, то рівняння граничної системи має вигляд

, при K ₁→∞.

Передатна функція ланки зворотного зв’язку має вираз

.

Таким чином, для структури, в якій зворотний зв’язок (ЗЗ) охоплює лише операційний підсилювач, ланка ЗЗ повинна мати властивості інтегральної ланки, враховуючи тим самим інтегральні властивості і параметри ВМ (K_ВМ, Т_ВМ).

2. Дослідимо властивості реального регулятора для випадку, коли коефіцієнт передачі ОП є кінцевим числом,тобто K ₁ ≠ ∞.

Еквівалентна передатна функція з’єднання ланок (рисунок 6.10) має вигляд:

.

Скоротимо чисельник і знаменник на Т_ВМ ∙ s, потім поділимо на K ₁∙ K_ВМ:

.

З’єднання ланок в даній граничній системі, що має властивості П-регулятора, може бути представлене у вигляді послідовного з’єднання двох умовних ланок: ланки з передатною функцією ідеального П-регулятора W_ІД^П(s) та баластної ланки W_БАЛ^П(s), що спотворює ідеальний П-закон регулювання, і властивості якої визначимо далі.

3. Визначимо властивості баластної ланки реального П-регулятора.

Передатна функція ідеального П-регулятора

.

Передатна функція баластної ланки П-регулятора є інерційною ланкою першого порядка з коефіцієнтом передачі :

при

де 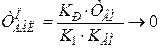при – постійна часу баластної ланки.

Т.ч. баластна ланка реального П-регулятора, як і в попередньому випадку реалізації регулятора, є інерційною ланкою першого порядку з одиничним коефіцієнтом передачі, постійна часу якої наближається до нуля в граничній системі, тобто при К ₁→ ∞ вона перетворюється в П-ланку і не спотворює закон регулювання.

Всі висновки з властивостей баластної ланки, КЧХ і ОНР, що наведені вище для випадку реалізації П-регулятора з охопленням ВМ постійної швидкості ЗЗ за схемою а) вірні і для випадку реалізації П-регулятора без охоплення ВМ ЗЗ за схемою б), тому їх потрібно наводити при аналізі властивостей даної баластної ланки в повному обсязі.

6.4 Реалізація ПІ-закону регулювання АР з ВМ постійної швидкості

а) з охопленням ВМ постійної швидкості зворотним зв’язком

Рисунок 6.10 – Структурна схема ПІ-регулятора з охопленням ВМ ЗЗ

1-й крок: визначимо тип ланки ЗЗ в ідеальному ПІ-регуляторі, для чого використаємо рівняння граничної системи:

.

Т.ч. знаходимо, що для формування ПІ-закону потрібно встановити у ЗЗ реальну диференційну ланку першого порядку (оператор Лапласа s в чисельнику і знаменнику) з постыйною часу Т ₁.

2-й крок: визначимо властивості такого реального регулятора, для чого запишемо еквівалентну передатну функцію за рисунком 6.10:

3-й крок: виділимо у виразі для W_ЕКВ (s) передатні функції ідеального ПІ-регулятора і його баластної ланки, для чого знаменник дробу приведемо до загального знаменника і скоротимо на s:

Поділимо чисельник і знаменник виразу на комплекс (Т_ВМ + K ₁ ∙K_ВМ∙K_ЗЗ∙Т ₁) і перегрупуємо рівніння таким чином, щоб виділити структуру, подібну до структури передатної функції ідеального ПІ-регулятора

,

Т.ч. реальний ПІ-регулятор можна представити, як послідовне з’єднання ідеального ПІ-регулятора і баластної ланки, тобто реальний ПІ-регулятор формує наближений регулювання.

4-й крок: дослідимо властивості реального ПІ-регулятора:

1) , де .

Параметри налаштування ПІ-регулятора К_Р і Т_И не є взаємозв’язаними, і визначаються лише параметрами ланки зворотного зв’язку.

2) Властивості баластної ланки:

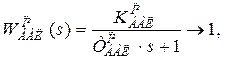при .

Висновок: баластна ланка – інерційна ланка першого порядку.

3) коефіцієнт передачі баластної ланки в граничній системі наближається до 1

при .

В реальному регуляторі, де K ₁ – кінцеве число, залежить від параметрів ВМ, від якості операційного підсилювача і від параметрів налаштування АР:

.

4) постійна часу баластної ланки в граничній системі наближається до 0.

,

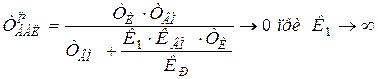тобто баластна ланка вироджується в пропорційну ланку з одиничним коефіцієнтом передачі і не спотворює закон регулювання.

1) в реальному регуляторі постійна часу баластної ланки залежить від всіх параметрів, що входять в формулу

а) б)

Рисунок 6.11 – Криві розгону (а) і ОНР реального ПІ-регулятора (б)

б) без охопленням ВМ постійної швидкості зворотним зв’язком

Рисунок 6.12 – Структурна схема АР без охоплення ВМ ЗЗ

1-й крок: визначимо передатну функцію ланки ЗЗ в ідеальному ПІ-регуляторі.

Оскільки ВМ має інтегральні властивості, і КПП включений послідовно з ним, то згідно з методом послідовної корекції, для формування ПІ-закону регулювання даною еквівалентною системою необхідно:

– для формування П-складової нейтралізувати інтегральні властивості ВМ диференційною ланкою;

– для формування І-складової потрібно лише промасштабувати інтегральні властивості ВМ П-ланкою.

Т.ч., КПП повинен формувати ПД-закон.

В граничній системі закон регулювання визначається в ланці ЗЗ, тому з рівняння нашої граничної системи можна записати:

.

2-й крок: визначимо еквівалентну передатну функцію структури для реального регулятора:

3-й крок: виділимо у виразі для W_ЕКВ (s) передатні функції ідеального ПІ-регулятора і його баластної ланки, для чого поділимо чисельник і знаменник на комплекс , виділимо структуру передатної функції ПІ-регулятора:

4-й крок: дослідимо властивості реального ПІ-регулятора:

Передатна функція ідеального ПІ-регулятора:

1. .

Висновки:

а) як і в попередньому випадку, постійна часу інтегрування (часу ізодрому) Т_И повністю визначається величиною постійної часу ланки ЗЗ Т ₁.

б) З виразу для коефіцієнта передачі регулятора К_Р видно, що параметри налагодження К_Р і Т_И взаємозв’язані:

.

в) – коефіцієнт передачі регулятора залежить: від коефіцієнта передачі ланки ЗЗ К_ЗЗ, параметрів ВМ (К_ВМ і Т_ВМ) і параметрів налаштування Т_И.

2. В граничній системі при баластна ланка також є інерційною ланкою першого порядку:

.

Властивості баластної ланки в граничній системі:

а) коефіцієнт передачі баластної ланки наближається до 1:

.

б) Постійна часу баластної ланки наближається до 0, тобто в граничній системі баластна ланка стає П-ланкою з одиничним коефіцієнтом передачі і не спотворює закон регулювання:

.

в) В реальному регуляторі при K ₁=const параметри баластної ланки залежать від параметрів налаштування автоматичного регулятора K_P і Т_И, виконавчого механізму K_ВМ, Т_ВМ і якості операційного підсилювача K ₁:

Криві розгону (а) і ОНР даного ПІ-регулятора (б) аналогічні попередньому випадку (рисунок 6.13):

а) б)

Рисунок 6.13 – Крива розгону і ОНР ПІ-регулятора

6.5 Реалізація лінійного ПІД-закону регулювання

а) з охопленням зворотнім зв’язком ВМ постійної швидкості:

Рисунок 6.14 – Структурна схема ПІД-регулятора з охопленням ВМ ЗЗ

В лінійних законах регулювання використовуються лінійні математичні операції: множення, ділення, додавання, інтегрування, диференціювання.

К ₁ – операційний підсилювач (його наявність приводить до утворення граничної системи, якщо ЗЗ негативний).

Оскільки в прямому ланцюзі знаходиться ОП, що охоплений негативним ЗЗ, то в граничній системі ПІД-закон регулювання формується в ланці ЗЗ. Тому:

1-й крок: визначимо передатну функцію ланцюга ЗЗ, що формує ПІД-закон:

Тут Т₁ і Т₂ – це постійні часу ланок ЗЗ.

2-й крок: визначимо еквівалентну передатну функцію структури для реального регулятора:

.

3-й крок: виділимо у виразі для W_ЕКВ (s) передатні функції ідеального ПІД-регулятора і його баластної ланки, для чого поділимо чисельник і знаменник на комплекс і приведемо вираз до загального знаменника:

.

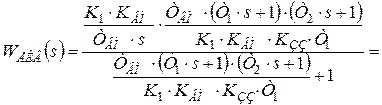
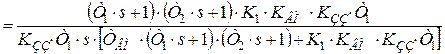виділимо передатні функції ПІД-регулятора і баластної ланки:

4-й крок: проаналізуємо властивості реального ПІД-регулятора при K ₁ = const.

1. Якщо позначити Т₁+Т₂ через параметр налаштування Т_И, то одержимо передатну функцію ідеального ПІД-регулятора:

,

, ,

Висновок 1: параметри налаштування Т_Д, Т_И, К_Р взаємозв’язані, тобто зміна одного з параметрів налаштування призводить до зміни інших.

2. Проаналізуємо властивості баластної ланки, для чого запишемо її передатну функцію у вигляді передатної функції інерційної ланки другого порядку:

а)

K ₁ у виразі для коефіцієнта передачі знаходиться і в чисельнику, і в знаменнику, тобто є невизначеність виду . Для граничної системи можна визначити , використавши правило Лопіталя (для чого і чисельник, і знаменник ділимо на K ₁), і перевести невизначеність у знаменник виразу. Звідки граничне значення для K ₁→∞.

Висновок 2: в граничній системі коефіцієнт баластної ланки наближається до одиниці.

б)

Висновок 3: в граничній системі постійна часу баластної ланки наближається до нуля.

Висновок 4: в реальному регуляторі при K ₁= const, перша постійна часу залежить від всіх параметрів, що входять до її виразу, а саме

в) Друга постійна часу баластної ланки зв’язана з першою постійною часу через вираз:

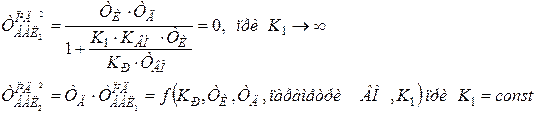
Висновок 5: постійні часу баластної ланки зв’язані між собою через параметр налаштування регулятора – постійну часу диференціювання Т_Д, тому можливі такі ситуації, коли інерційна ланка другого порядку стає нестійкою.

В залежності від співвідношення і можливі 4 види кривих розгону інерційної ланки другого порядку (рисунок 6.15):

г) .

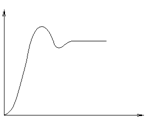
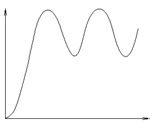
а) б) в) г)

Рисунок 6.15 – Криві розгону інерційних ланок другого порядку

Висновок 6: в залежності від співвідношення і можливі стійкі і нестійкі перехідні процеси в баластній ланці, причому вигляд перехідних процесів залежить від значення Т_Д.

3. Визначимо граничне співвідношення між параметрами Т_И і Т_Д:

Як було показано раніше, Т_Д і Т_И зв’язані між собою через параметри ланки ЗЗ Т ₁ і Т ₂, тому можна записати:

,

оскільки Т ₁ і Т ₂входять і в чисельник і в знаменник, то визначимо граничне значення цього відношення:

.

Висновок 7: максимальне співвідношення Т_Д/Т_И можливо лише при Т ₁ = Т ₂, у інших випадках відношення буде менше 0,25, тобто Т_Д/Т_И ≤ 0,25.

4. Визначимо характеристики перехідних процесів у баластній ланці.

З дисципліни ТАУ відомо, що характер перехідного процесу залежить від значення коренів характеристичного рівняння.

Визначимо корені характеристичного рівняння.

Характеристичне рівняння будь-якої ланки записується шляхом прирівнення нулю знаменника передатної функції і заміни оператора Лапласа на літеру «р»:

.

Визначимо дискримінант квадратного рівняння і, якщо його корні дійсні, то ланка стійка, якщо корні уявні – ланка нестійка:

.

Вираз у перший дужці завжди позитивний, тому ми визначимо знак виразу в другій дужці:

Т.ч., вираз у другій дужці завжди від’ємний при будь-яких Т ₁ і Т ₂.

Висновок 8: дискримінант характеристичного рівняння від’ємний, корні характеристичного рівняння містять реальну і уявну частину, тому ця баластна ланка є інерційною ланкою другого порядку з коливально-затухаючим перехідним процесом. Крива розгону даного ідеального ПІД-регулятора має вигляд, зображений на рисунку 6.16,а.

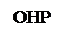
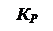
а) б)

Рисунок 6.16 – Крива розгону (а) і його ОНР (б) реального ПІД-регулятора

Висновок 9: при кінцевих значеннях коефіцієнта передачі ОП K ₁ крива розгону ПІД-регулятора може бути коливальною затухаючою, а при нескінченно великих значеннях коефіцієнта ОП K ₁крива розгону буде близькою до ідеальної.

Тобто, для формування ПІД-закону в промислових регуляторах необхідно використовувати високоякісні операційні підсилювачі.

ОНР для ПІД-регулятора з трьома параметрами налаштування є тривимірною фігурою і її потрібно графічно зображувати у трьох координатах K_Р, Т_И, Т_Д. Для того, щоб перейти до двовимірного зображення, використовують накладання перетинів при фіксованих Т_Д (рисунок 6.16,б). Для кожного значення Т_Д можна знайти дозволені значення K_Р, при яких ∆M(ω) < 10%, а ∆Θ(ω) < 15º, де ∆M(ω) – різниця між модулями КЧХ реального і ідеального ПІД-регулятора, ∆Θ(ω) – різниця між фазами КЧХ.

б) без охоплення зворотнім зв’язком ВМ постійної швидкості

Оскільки ВМ не охоплений зворотнім зв’язком, і за своєю природою є інтегральною ланкою, то, виходячи з методу послідовної корекції, КПП повинен формувати ПДД²-закон перетворення вхідного сигналу (рисунок 6.17).

1-й крок. Оскільки ми використовуємо граничну систему в КПП, то визначимо передатну функцію ланцюга ЗЗ:

рисунок 6.17 – Структурна схема ПІД-регулятора без охопленням ВМ ЗЗ

.

якщо винести за дужки K_П і позначити його як 1/ K_ЗЗ, то знаменник можливо записати як рівняння другого порядку, т.ч. можна стверджувати, що в ЗЗ граничної системи потрібно встановити інерційну ланку другого порядку з аперіодичною кривою розгону.

Поиск по сайту: