В ТВЕРДОМ ТЕЛЕ

Цель данной лекции состоит в объяснении механизма образования энергетических зон в твердом теле, для чего используется два альтернативных подхода – приближение сильно связанных (квазисвязанных) электронов и приближение почти свободных (квазисвободных) электронов.

В рамках приближения сильно связанных электронов принимается, что зонная структура твердого тела образуется в результате уширения энергетических уровней атомов, составляющих кристалл.

Считается, что энергетический спектр изолированного атома нам известен и характеризуется уравнением Шредингера:

; (2.1)

, (2.2)

где - потенциальная энергия электрона в изолированном атоме.

При переходе от изолированного атома к кристаллу в первую очередь необходимо учесть изменение потенциальной энергии :

. (2.3)

Соответственно, гамильтониан кристалла имеет вид:

H_g = H_a + W (r). (2.4)

С другой стороны, для кристалла волновая функция электрона 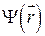должна иметь вид блоховской волны:

, (2.5)

где - вектор, соединяющий два соседних атома.

Поскольку для кристалла

, (2.6)

то с учетом энергии возмущения:

. (2.7)

Так как не только , но и является собственной функцией гамильтониана H_a и, соответственно,

, (2.8)

то уравнение (2.7) упрощается:

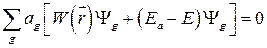. (2.9)

Следуя стандартным операциям анализа уравнения Шредингера, умножим выражение (2.9) на комплексно-сопряженную функцию , где индекс означает принадлежность ее к соседнему атому по сравнению с атомом g, и проинтегрируем по всему объему кристалла t:

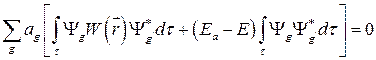. (2.10)

В этом выражении обменный интеграл

(2.11)

характеризует обменную энергию взаимодействия и зависит от степени перекрывания волновых функций атомов и от энергии возмущения.

Второй интеграл:

(2.12)

называется интегралом неортогональности или интегралом перекрытия, причем S_gg = 1 (в этом случае – это просто нормировочный интеграл для ), а при он, хотя и мал по сравнению с единицей, но не равен нулю.

С учетом введенных обозначений (2.11) и (2.12) уравнение (2.10) можно представить в виде:

. (2.13)

Поскольку в приближении сильно связанных электронов при и при , то член в знаменателе

. (2.14)

С другой стороны, при для интеграла в числителе можно записать:

, (2.15)

где С - константа, не зависящая от . Фактически, С представляет собой усредненную для некоторого атома потенциальную энергию электрона в поле всех остальных ядер с учетом самосогласованного характера поля.

В итоге, уравнение (2.13) приобретает вид:

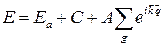(2.16)

Рассмотрим физический смысл этого соотношения на примере простой кубической ячейки с периодом . Очевидно, что вокруг некоторого произвольно взятого узла с соседние узлы будут расположены на расстоянии , причем у каждого узла будут по шесть ближайших соседей. В этом случае

. (2.17)

Соответственно, энергия электрона в периодическом поле прстой кубической решетки равна:

. (2.18)

Очевидно, что экстремальные значения энергии будут иметь место при cosk_xa = ±1, cosk_ya = ±1, cosk_za = ±1:

; , (2.19)

и, соответственно:

. (2.20)

Из полученных соотношений следует, что при образовании кристаллической решетки в результате взаимодействия атомов происходит смещение уровня изолированного атома на величину С. Одновременно ансамбль атомных уровней расщепляется в полосу (зону), внутри которой энергия электронов является периодической функцией компонентов волнового вектора . Для простой кубической решетки эти зоны разрешенной энергии имеют ширину 12 А, то есть определяются величиной обменного интеграла.

Важно, что поскольку величина интеграла есть функция перекрывания электронных облаков соседних атомов, то чем выше степень такого перекрывания, тем шире энергетическая зона разрешенных энергий. Поэтому более высоко расположенные атомные уровни из–за большего перекрывания их волновых функций образуют более широкие энергетические зоны.

Как видно из энергетической диаграммы (рис. 2.1), разрешенные энергетические зоны в общем случае разделены запрещенными интервалами энергий (запрещенными зонами Е_g), ширина которых снижается при переходе от внутренних электронных оболочек к наружным. При больших значениях энергии разрешенные зоны могут накладываться (перекрываться).

Рис. 2.1. Образование зонной структуры твердого тела в модели сильно связанных электронов.

Внешние воздействия, вызывающие изменение расстояния между узлами решетки (сжатие или растяжение, нагрев), естественно, приводят к изменению области перекрывания волновых функций, и в результате изменения обменного итеграла вызывают изменение ширины разрешенных и запрещенных зон.

Альтернативой рассмотренной выше модели сильно связанных электронов является модель квазисвободных электронов, в рамках которой принимается, что периодическое поле решеточных остовов действует на валентные электроны лишь как слабое возмущение. Поэтому зависимость энергии электрона от волнового вектора в кристалле аналогична таковой для свободного электрона, то есть соответствует параболическому закону дисперсии:

E = ħ²k²/2m. (2.21)

Однако, при условии, когда , где - целое число, электронная волна претерпевает брэгговское отражение и, как результат, резко усиливается ее взаимодействие с полем периодического потенциала остовов. Первое отражение имеет место для , второе – для и т.д.

Ограничиваясь рассмотрением первого отражения, проанализируем вид волновой функции электрона в кристалле. Наличие брэгговской дифракции обусловливает то, что при условии электронная волна является стоячей. Существование такой стоячей волны возможно лишь в том случае, если она будет состоять из двух бегущих волн свободного электрона вида и 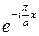, движущихся в противоположных направлениях (рис. 2.2).

Рис. 2.2. Координатная зависимость плотности вероятности ρ для волновых функций Ψ⁺ и Ψ^- в линейном идеальном кристалле.

На основе этих двух бегущих волн можно получить две стоячие волны:

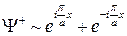; (2.22)

. (2.23)

Из формулы Эйлера следует, что:

; (2.24)

. (2.25)

В уравнениях (2.22) – (2.25) знак пропорциональности вместо знака равенства стоит из–за того, что для упрощения не вводится условие нормировки.

Для определения координатной зависимости плотности заряда ρ (определяющей, фактически, координатное положение электронов) найдем квадрат модуля волновых функций (2.24) и (2.25):

; (2.26)

. (2.27)

Из этих соотношений видно, что электроны могут располагаться в линейном кристалле двумя разными способами: в областях, где потенциальная энергия минимальна , то есть непосредственно на положительных ионах (функция 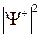), и в промежутках, точно посередине между остовами (функция ), что показано на рис. 2.2.

Таким образом, волновая функция Ψ⁺, давая максимумы плотности заряда вблизи положительных ионов, понижает потенциальную энергию относительно ее среднего уровня, а функция Ψ^-, напротив, ее повышает. В результате, средние значения потенциальной энергии для функций ρ⁺ и ρ^- различаются на некоторую величину (энергетическую щель), называемую запрещенной зоной с шириной, обозначаемой E_g (рис. 2.3).

Рис. 2.3. Зависимость энергии от волнового вектора для свободного электрона (а) и для электрона в решетке (б).

Поиск по сайту: