КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ

Наряду с электронной подсистемой, поведение твердых тел в различного рода химических, термо-, фотохимических и других процессах определяется колебательной, или фононной, подсистемой. Колебания решетки – согласованные колебательные смещения структурных элементов кристалла относительно их положений равновесия. Если амплитуда колебаний намного меньше постоянной решетки, колебания являются гармоническими (нормальными), с видом плоской волны, характеризующейся волновым вектором . Квант энергии колебания решетки называется фононом.

В трехмерной решетке смещения атомов можно описать как суперпозицию нормальных колебаний, каждое из которых характеризуется своим - вектором, длиной волны l либо частотой . Волновой - вектор имеет столько разрешенных значений, сколько в кристалле содержится элементарных ячеек, и изменяется в пределах зоны Бриллюэна , где - постоянная решетки, . Поскольку каждый атом обладает тремя степенями свободы, то общее чис ло степеней свободы в кристалле равно , где - число атомов в одной элементарной ячейке, 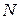- число элементарных ячеек в кристалле. Именно это же количество () волн и содержится в кристалле. Если учесть, что каждая из этих волн может быть представлена как гармонический осциллятор с энергией

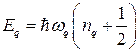, (5.1)

где - энергия нулевых колебаний, то полная энергия колебаний в кристалле равна:

. (5.2)

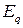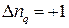Квантовый осциллятор с энергией (уравнение 5.2) может изменять свою энергию на величину , где. Соответствующий квант энергии колебаний решетки – фонон, равен , причем процесс с означает рождение фонона, а с - его уничтожение. Фактически, фонон можно рассматривать как единичное квантовое возбуждение определенного нормального колебания. По аналогии с фотоном, фонон также можно представить как носитель кванта энергии колебаний решетки, то есть как квазичастицу (в рамках гипотезы корпускулярно – волнового дуализма).

Фононы подчиняются статистике Бозе-Эйнштейна:

, (5.3)

где 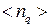- среднее число фононов в данном нормальном колебании с энергией фононов в условиях теплового равновесия, 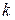- постоянная Больцмана.

Поскольку в приближении гармонических колебаний колебательная часть энергии кристалла равна аддитивной сумме энергий фононов , колебательное состояние кристалла может быть представлено как “идеальный газ фононов” (квазичастиц, не взаимодействующих друг с другом).

На основании распределения Бозе – Эйнштейна (5.3) можно полагать, что при Т = 0 К концентрация фононов в кристалле должна быть нулевой. Однако, в действительности, квантовая природа колебаний решетки обуславливает существование “нулевых колебаний” атомов даже при Т = 0 К. В частности, в кристалле гелия “нулевые колебания” приводят к тому, что твердый кристаллический гелий при Т ® 0 К существует лишь при давлении, превышающем 25 атм. При снижении давления он плавится, превращаясь в так называемую квантовую жидкость. В целом же, очевидно, что амплитуда колебаний при сверхнизких температурах незначительна, хотя и отлична от нуля.

При фононный газ заключает в себе практически основную часть тепловой энергии кристалла. В окрестностях этого температурного диапазона имеет место близкий к линейному рост числа фононов с увеличением температуры. Этим обстоятельством можно объяснить известное эмпирическое правило Дюлонга и Пти, согласно которому молярная теплоемкость при постоянном объеме для всех простых тел одинакова и приблизительно равна 25 Дж/моль×К. Действительно, учитывая, что число колебательных степеней свободы у кристалла равно ( - число Авогадро), средняя энергия теплового движения на 1 моль вещества составляет , а соответствующая мольная теплоемкость равна Дж/моль×К.

При понижении температуры теплоемкость падает гораздо ниже того значения, которое дает правило Дюлонга и Пти, устремляясь к нулю, как функция Т³ для диэлектриков, и линейно снижается с температурой для металлов. Правило Дюлонга и Пти справедливо для температуры выше - температуры Дебая (характеристической температуры в твердом теле, вводимой соотношением , где - максимальная частота колебаний кристаллической решетки, определяемая из условия равенства числа колебаний, приходящихся на частотный интервал от 0 до , полному числу колебательных степеней свободы решетки), когда возбуждены все колебательные степени свободы. При имеет место “вымораживание” все большего числа степеней свободы и, соответственно, снижение . Вследствие этого для таких материалов, как алмаз () и бериллий () значения существенно ниже предсказываемых правилом Дюлонга и Пти даже при комнатной температуре.

Максимальная энергия фононов имеет величину порядка , а минимальная длина волны фонона соответствует наибольшему значению волнового числа 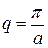. В простейшем случае дискретной одномерной цепочки атомов очевидно, что 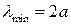, поскольку, естественно, что в дискретной цепочке не могут существовать волны с длиной полуволны меньшей, чем период решетки. В результате, для колебаний дискретных атомных структур характерно наличие предельной частоты фононов. Поскольку в твердых телах скорость звука см/с, 3×10^{-8 см, предельная частота фононов - величина порядка 2}×10¹³ Гц.

В трехмерном кристалле имеется два типа упругих волн: продольные (деформация сжатия – растяжения) и поперечные (деформация сдвига). Очевидно, что поперечные волны в каждой плоскости имеют два главных направления, поскольку эти колебания можно разложить на две независимые поперечные волны со взаимно перпендикулярными направлениями. В итоге, кристалл, содержащий атомов в элементарной ячейке, характеризуется наличием типов поперечных волн и типов продольных волн, то есть суммарно наличием различных типов (ветвей) колебаний.

Три ветви колебаний, для которых фазовая скорость равна групповой скорости и равна скорости звука, называются акустическими. Для них частота продольных колебаний выше, чем частота поперечных. Остальные ветви называются оптическими, для которых при фазовая скорость стремится к бесконечности, а групповая – к нулю.

Графически акустические и оптические фононы в приближении для цепочечного кристалла с представлены на рис. 5.1. Как видно из рисунка, оптические фононы обусловлены встречным колебательным движением атомов двух сортов (“черные” и “белые”). Очевидно, что если эти атомы различаются по своему электрическому заряду, то изменение расстояния между ними будет приводить к изменению дипольного момента, что в свою очередь может проявляться в поглощении и испускании ИК – излучения. Поэтому такого типа колебания были названы оптическими.

Для примера на рис. 5.1 приведены дисперсионные кривые (зависимость фононной частоты от волнового вектора ) для кристаллов кремния. Поскольку в ячейке Вигнера – Зейтца кремния имеется два атома, эти кривые содержат как акустические, так и оптические ветви (LA – продольная акустическая, LO – продольная оптическая, TA – поперечная акустическая, TO – поперечная оптическая).

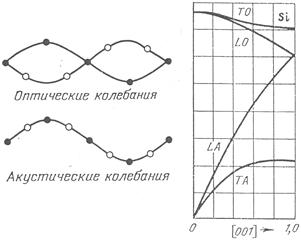
Рис. 5.1. Колебания узлов решетки, обусловливающие возникновение акустических (а) и оптических (б) фононов; типичные дисперсионные кривые для фононов (в)

Количество ветвей определяется наличием трех продольных акустических (по трем осям), трех продольных оптических, и в два раза больше поперечных (связанных с деформацией сдвига во взаимно перпендикулярных направлениях в каждой из трех плоскостей) акустических и оптических фононов. Однако ввиду наличия достаточно высокой симметрии у кристалла, часть колебаний оказывается вырожденной, а на дисперсионной кривой в кристаллографическом направлении [100] видны ветви ТО и ТА (обе дважды вырожденные), LO и LA. Характерно, что на краях зоны Бриллюэна, то есть когда 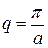, различия между оптическими и акустическими колебаниями минимальны.

Для определения параметров фононного спектра используются методы поглощения нейтронов либо фотонов. При поглощении фотонов (в ИК области), обычно, происходит резонансное превращение фотона в оптический фонон, причем на спектре поглощения обычно регистрируются комбинационные частоты (LO + TA, TO + LO и др.).

Фононы в твердых телах могут взаимодействовать как между собой, так и с другими квазичастицами, а также с дефектами кристаллической решетки. Взаимодействие фононов между собой можно рассматривать как проявление ангармонизма колебаний, приводящего к рождению новых фононов, либо напротив, к их аннигиляции, рассеянию друг на друге с изменением частоты и поляризации. Такого рода взаимодействия объясняют факт теплового расширения твердых тел, зависимость упругих постоянных от температуры и давления, различие между температурными зависимостями теплоемкостей С_р и С_v, и в целом, являются основным фактором, посредством которого устанавливается термодинамически равновесное распределение фононов.

Фонон-фононное взаимодействие в совокупности с дефектами кристаллической решетки ограничивает длину свободного пробега фононов, что, в свою очередь, определяет решеточную теплопроводность неметаллических кристаллов, являющуюся, фактически, теплопроводностью фононного газа.

При взаимодействии фононов с другими квазичастицами, например, с электронами зоны проводимости, фононы могут выполнять функцию “стока” для энергии, запасенной этими квазичастицами, и фактически, играют роль своеобразного внутреннего “термостата”. Именно через фононы, как правило, происходит связь квазичастиц со всеми остальными компонентами твердого тела.

Поиск по сайту: