Lsolve(A,B),

которая возвращает вектор Х для системы линейных уравнений А*Х=В при заданной матрице коэффициентов А и векторе свободных членов В.

На рис.64 приведены примеры применения функции lsolve.

Рис.64. Пример символьного решения системы линейных уравнений с применением функции lsolve

5. Решение систем линейных уравнений в матричной форме.

Векторные и матричные операторы и функции системы MathCad позволяют решать широкий круг задач линейной алгебры.

Для системы линейных уравнений А*Х=В при заданной матрице коэффициентов А и векторе свободных членов В вектор решения можно получить из очевидного выражения Х=В*А .

На рис.65 приведен пример решения систем линейных уравнений в матричной форме.

Рис.65. Пример матричного решения системы линейных уравнений

6. Решение нелинейных уравнений и их систем

При решении нелинейных уравнений и их систем используется специальный вычислительный блок, открываемый служебным словом-директивой Given, которое набирается с клавиатуры. До начала блока задаются начальные приближения к неизвестным переменным. Внутри блока записывается уравнение или система уравнений. Для решения систем нелинейных уравнений используется одна из двух следующих функций:

find(v1,v2...vn) - возвращает значение одной или нескольких переменных для точного решения;

minerr(v1,v2...vn) - возвращает значение одной или нескольких переменных для приближенного решения.

Между этими двумя функциями существуют принципиальные различия. Первая функция используется, когда решение реально существует (хотя и не является аналитическим). Вторая функция пытается найти максимальное приближение даже к несуществующему решению путем минимизации среднеквадратичной погрешности решения.

На рис. 66 и 67 приведены примеры применения функции find и minerr для решения уравнений и систем уравнений.

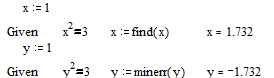
Рис.66. Пример решения нелинейных уравнений с помощью функций find и minerr

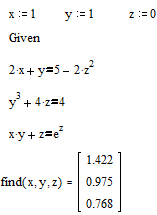
Рис.67. Пример решения систем нелинейных уравнений с помощью функций find и minerr

Поиск по сайту: