Теоретическая часть. Пользуясь описанными в ранее проведенных лабораторных работах приемами выполнения простейших расчетов и построения графиков функций в Excel

Пользуясь описанными в ранее проведенных лабораторных работах приемами выполнения простейших расчетов и построения графиков функций в Excel, можно находить решение различных математических задач. Рассмотрим это на примере наиболее часто встречающихся задач нахождения корней нелинейных уравнений и решения систем линейных уравнений. Указанные математические задачи легко решаются с помощью надстроек Excel «Поиск решения» и «Подбор параметра».

Надстройка Microsoft Excel «Подбор параметра» служит для нахождения оптимального желаемого решения за счет изменения одного из параметров. С формальной точки зрения такие задачи описываются уравнением с одной переменной, которое в общем случае можно представить в следующем каноническом виде:

F(x)=0, где функция F(x) определена и непрерывна на интервале [a,b]. Таким образом, можно сказать, что инструмент «Подбор параметра» служит для нахождения корня уравнения x. В этой надстройке реализован алгоритм метода половинного деления.

Пример. Решим уравнение x²-3=0, используя надстройку «Подбор параметра».

В ячейку А1 вводится начальное приближение для поиска одного из корней уравнения. Лучше найти его графически, хотя можно подставить и произвольное значение (например, ноль). В ячейку В2 записывается в виде формулы левая часть решаемого уравнения. Диалоговое окно данного инструмента вызывается через меню Данные/Подбор параметра и имеет следующий вид (рис. 43, 44):

Рис. 43. Надстройка «Подбор параметра»

Рис. 44. Надстройка «Подбор параметра»

В поле Установить в ячейке вводится ссылка на ячейку, содержащую левую часть уравнения. В поле Значение непосредственно (т.е. без ссылок на ячейки) вводится правая часть уравнения. Причем правая часть уравнения должна обязательно представлять собой конкретное числовое значение. Если правая часть уравнения содержит переменную или какое-либо выражение, то такое уравнение должно быть предварительно преобразовано к равносильному виду (в общем случае к каноническому виду F(x)=0). Нажав кнопку ОК, получаем в ячейке А1 значение искомого корня: 1,731856.

Нелинейные уравнения также можно решать, используя надстройку «Поиск решения». Для того чтобы ее подключить, следует в меню Office (рис. 45)

Рис. 45. Надстройка «Поиск решения»

выбрать пункт Параметры Excel (рис. 46)

Рис. 46. Надстройка «Поиск решения»

и в раскрывшемся списке войти в меню Надстройки, далее активировать Поиск решения и установить флажок против пункта Поиск решения (рис. 47).

Рис. 47. Надстройка «Поиск решения»

После нажатия кнопки ОК соответствующий значок появится во вкладке Данные (рис. 48).

Рис. 48. Надстройка «Поиск решения»

В ячейку А1 заносится начальное приближение корня, в ячейку В1 - левая часть уравнения в виде формулы. Для предыдущего примера она имеет вид =А1*А1-3.

Далее из вкладки меню Данные запускается надстройка Поиск решения.

В открывшемся диалоговом окне Поиск решения устанавливается целевая ячейка $B$1 равная нулевому значению. В текстовом поле Изменяя ячейки устанавливается адрес $А$1 и нажимается кнопка Выполнить (рис. 49).

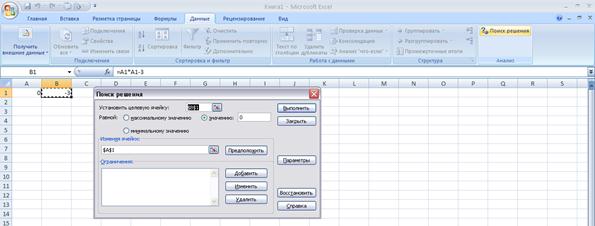
Рис. 49. Надстройка «Поиск решения»

В ячейке А1 получается значение корня 1,732051 (рис. 50).

Рис. 50. Результаты работы надстройки «Поиск решения»

Как видим, оно совпало с точностью до 0,001 с найденным ранее значением.

Обращает на себя внимание неточность решения. Мы получаем очень близко приближающиеся к точным, но все же неточные корни уравнения. Это происходит потому, что решение уравнений на вычислительной технике происходит не аналитическими методами, как это делает человек, а специально разработанными методами, получившими название численных. В отличие от аналитических (точных) методов, численные методы обладают определенной погрешностью. В Excel с целью повышения точности решения пользователь может уменьшить погрешность вычислений, но при этом может потребоваться увеличение количества итераций. При этом надо помнить, что тем самым увеличивается время на поиск решения. Установленные по умолчанию значения, подходят для большинства практических задач. По умолчанию, относительная погрешность вычислений и составляет 0,001 (рис. 51).

Рис. 51. Изменение погрешности

Следует отметить, что найден только один из двух корней данного уравнения. Для нахождения второго корня, следует в ячейку А1 ввести новое приближение, близкое ко второму корню, и повторить поиск решения.

Для того, чтобы использовать рассматриваемую надстройку Поиск решения для нахождения решения системы линейных алгебраических уравнений, следует ввести в столбец А начальное приближение для значений всех неизвестных. Пусть это будут нули. В столбец В ввести формулы, описывающие левые части уравнений. В столбец С вводят значения правых частей уравнений. Курсор ставят на ячейку В1 и запускают надстройку Поиск решения. Значение целевой ячейки $B$1устанавливают равным значению ячейки С1. Изменяют значения ячеек столбца А. К ограничениям добавляют все уравнения, кроме первого. Для системы уравнений

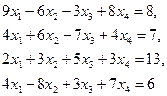
настроенный на показ формул лист Excel, с диалоговым окном Поиск решения будут выглядеть так, как это показано на рисунке (рис. 52, 53).

Рис. 52. Надстройка «Поиск решения»

Рис. 53. Надстройка «Поиск решения»

Нажав кнопку Выполнить, получается в столбце А значение неизвестных (рис. 54):

.

Рис. 54. Результаты работы с надстройкой «Поиск решения»

Как видно, надстройка Поиск решения очень удобна для решения рассмотренных задач. Однако следует помнить, что алгоритмы, реализованные в ней, предназначались не для них, а для решения задач оптимизации. Поэтому возможны сбои в работе надстройки, и к полученным результатам необходимо подходить критически.

Поиск по сайту: