 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Основные теоретические положения. 2.1. Последовательное соединение элементов цепи
2.1. Последовательное соединение элементов цепи.
В случае последовательного соединения элементов цепи R, L, C мгновенное значение приложенного напряжения равно сумме мгновенных значений падений напряжений на участках цепи

|

В случае линейных параметров R, L, C, при подключении электрической цепи к синусоидальному напряжению  в ней будет протекать также синусоидальный ток
в ней будет протекать также синусоидальный ток 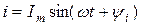 . Причем, начальную фазу тока
. Причем, начальную фазу тока  . Тогда начальная фаза напряжения
. Тогда начальная фаза напряжения  будет равна углу сдвига фаз
будет равна углу сдвига фаз 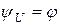 и выражение для напряжения запишется в виде
и выражение для напряжения запишется в виде  .
.
Тогда выражение (1) можно записать в виде
|

Из (2) следует, что падение напряжения на активном сопротивлении 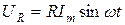 совпадает по фазе с током
совпадает по фазе с током  , а амплитуда напряжения
, а амплитуда напряжения  .
.
На индуктивности падение напряжения  опережает ток на четверть периода
опережает ток на четверть периода  Величина
Величина  называется индуктивным сопротивлением и амплитуда напряжения на индуктивности
называется индуктивным сопротивлением и амплитуда напряжения на индуктивности 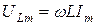 .
.
На емкости падение напряжения  отстает от тока на четверть периода
отстает от тока на четверть периода  . Величина
. Величина  называется емкостным сопротивлением и амплитуда падения напряжения на емкости
называется емкостным сопротивлением и амплитуда падения напряжения на емкости  .
.
Так как напряжение отстает от тока на 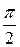 , то эти напряжения находятся в противофазе и, следовательно, компенсируют друг друга. В связи с этим принято считать индуктивные сопротивления
, то эти напряжения находятся в противофазе и, следовательно, компенсируют друг друга. В связи с этим принято считать индуктивные сопротивления  , а емкостные
, а емкостные  .
.
Можно отметить, что индуктивные сопротивления  и емкостные сопротивления
и емкостные сопротивления  являются формальными величинами, существующими только при синусоидальной форме тока и напряжения.
являются формальными величинами, существующими только при синусоидальной форме тока и напряжения.
Физическими сопротивлениями для индуктивности являются процессы индуктирования ЭДС, а для емкости – процессы поляризации диэлектриков и образование токов смещения.
Преобразуя определенным образом выражение (2) получим:
 ,
,
|
 ,
,
где U, I – действующие значения.
Выражение  - называется реактивным сопротивлением цепи. Очевидно, если
- называется реактивным сопротивлением цепи. Очевидно, если  , то цепь имеет индуктивный характер,
, то цепь имеет индуктивный характер, 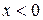 - емкостной.
- емкостной.
Величина  называется полным сопротивлением цепи.
называется полным сопротивлением цепи.
Тогда  .
.
Сдвиг по фазе между током и напряжением:
|

Итак, связь между током и напряжением при последовательном соединении R, L, C определяется выражениями:
|


Необходимо подчеркнуть, что при определении любой величины в цепи переменного синусоидального тока необходимо определять всегда две ее характеристики – амплитуду и фазу.
Используя изображение синусоидальных величин вращающимися векторами на плоскости, по уравнению (2) можно построить векторную диаграмму последовательной цепи.
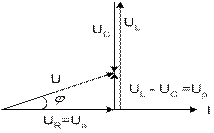
Рис.1
Для последовательной цепи можно привести треугольники напряжений и сопротивлений

Рис.2
Из треугольника можно получить соотношение:
|
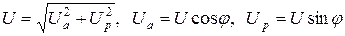

В вышеприведенных соотношениях параметры R, L, C считались идеальными.
В реальных элементах это справедливо только для активных сопротивлений и емкостей.
Индуктивность, в силу своего конструктивного исполнения, нельзя считать идеальной. Катушка индуктивности всегда характеризуется и индуктивным и активным сопротивлением.
Эквивалентную схему катушки индуктивности можно представить в виде
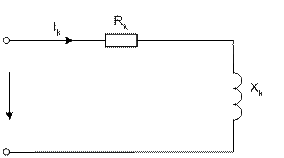
Рис.3
и, следовательно, имеем:
 .
.
Отношение 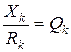 - называется добротностью катушки.
- называется добротностью катушки.
|


Рис.4
Средняя, за период, мощность называется активной мощностью
 .
.
Выражение  называется полной мощностью.
называется полной мощностью.
При синусоидальных токах и напряжениях вводят понятие реактивной мощности
 .
.
Тогда можно получить треугольник мощностей

и соотношения
 .
.
Отношение активной мощности к полной называется коэффициентом мощности цепи.
 .
.
Для вычисления мощностей применяют выражения:

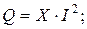
 .
.
2.2. Параллельное соединение элементов цепи.

Рис.5
По закону Кирхгофа
|

При синусоидальном напряжении  ток на входе цепи так же будет синусоидальным
ток на входе цепи так же будет синусоидальным  .
.
И тогда уравнение (8) перепишется в виде:
|
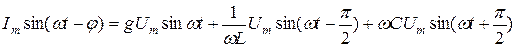
Из (9) можно получить

|
 ,
,
где g – активная проводимость;
 - индуктивная проводимость;
- индуктивная проводимость;
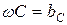 - емкостная проводимость;
- емкостная проводимость;
 - реактивная проводимость;
- реактивная проводимость;
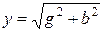 - полная проводимость цепи.
- полная проводимость цепи.
По уравнению (9) можно построить векторную диаграмму

Рис.6
Для параллельного соединения можно привести треугольники токов и проводимостей
| |||
| |||
Любую цепь с последовательным соединением приемников можно заменить эквивалентной ей цепью с параллельным соединением и наоборот.
Если заданы сопротивления последовательной цепи R, X, Z, то эквивалентные проводимости определяются следующим образом:


 .
.
Если наоборот заданы y, g, b, то будем иметь эквивалентные сопротивления:
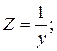

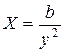 .
.
2.3. Смешанное соединение элементов цепи.
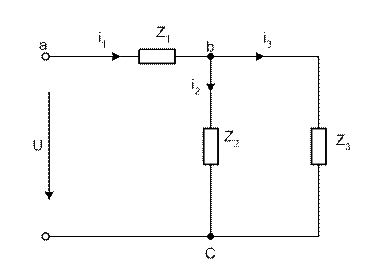
Рис.7
При смешанном соединении элементов процессы в цепи описываются первым и вторым законами Кирхгофа. Для цепи рис.7 имеем:
 ,
,

или в векторной форме:

 .
.
Рассмотрим, как, используя векторную диаграмму, можно определить параметры цепи напряжения или тока.
Пусть задана схема
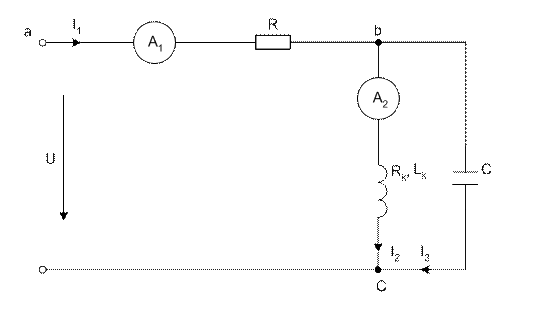
Рис.8
В цепи измерены вольтметром действующие значения напряжений 
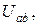
 и амперметром действующие значения токов
и амперметром действующие значения токов 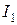 и
и  . Необходимо определить ток
. Необходимо определить ток  и параметры цепи.
и параметры цепи.
Строим векторную диаграмму следующим образом. Выбираем масштабы для напряжений и токов. Затем задаем вектор напряжения  . Из точки (b) радиусом
. Из точки (b) радиусом  проводим окружность, а из точки (с) радиусом
проводим окружность, а из точки (с) радиусом  делаем засечки на окружности радиуса
делаем засечки на окружности радиуса  . Получаем точки
. Получаем точки 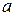 и
и 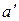 на векторной диаграмме, и следовательно, положение векторов напряжений
на векторной диаграмме, и следовательно, положение векторов напряжений 
 ,
,  . Строим вектора токов. Направление тока совпадает с направлением напряжения
. Строим вектора токов. Направление тока совпадает с направлением напряжения 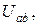 так как на участке
так как на участке 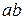 находится активное сопротивление R. Из точки
находится активное сопротивление R. Из точки  откладываем вектор тока
откладываем вектор тока  . Направление тока
. Направление тока  неизвестно, но известна его величина. Из точки
неизвестно, но известна его величина. Из точки  проводим окружность радиуса
проводим окружность радиуса  .
.
Через конец вектора 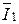 проводим перпендикуляр
проводим перпендикуляр  . Тогда отрезок
. Тогда отрезок  будет ток
будет ток  , а отрезок
, а отрезок 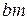 - ток
- ток  , так как в заданной схеме
, так как в заданной схеме 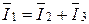 .
.

Рис.9
Теперь из векторной диаграммы можно определить угол сдвига фаз  на входе цепи, т.е. между напряжениями
на входе цепи, т.е. между напряжениями  и током
и током  .
.

Угол сдвига фаз на катушке  будет равен
будет равен
 .
.
Тогда параметры цепи определяются следующим образом:
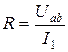 ;
;  ;
; 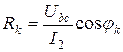 ;
;  .
.
Емкость  , индуктивность
, индуктивность 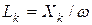 , где
, где  эквивалентное активное сопротивление всей цепи
эквивалентное активное сопротивление всей цепи  , и эквивалентное реактивное
, и эквивалентное реактивное  .
.
Отметим одну особенность при построении векторной диаграммы. При пересечении окружностей радиусов  и
и  получим два положения для точки а. Положение
получим два положения для точки а. Положение 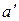 не удовлетворяет решению, так как фазовые углы сдвига не соответствуют характеру нагрузки на участках цепи. На диаграмме ток
не удовлетворяет решению, так как фазовые углы сдвига не соответствуют характеру нагрузки на участках цепи. На диаграмме ток  отстает от напряжения, а должен опережать, так это ток емкости. Ток
отстает от напряжения, а должен опережать, так это ток емкости. Ток  опережает напряжение
опережает напряжение  , а должен отставать, так как это ток в индуктивности. В данной схеме удовлетворяет решению положение точки
, а должен отставать, так как это ток в индуктивности. В данной схеме удовлетворяет решению положение точки  .
.
Поиск по сайту:






