Основные теоретические положения. Резонансом напряжение называют такой режим цепи с последовательным соединением элементов , когда полное сопротивление равно активному

Резонансом напряжение называют такой режим цепи с последовательным соединением элементов , когда полное сопротивление равно активному, несмотря на наличие реактивных сопротивлений. При этом ток совпадает по фазе с приложенным напряжением, а напряжения на реактивных элементах цепи равны по величине и противоположны по фазе.

Следовательно, для режима резонанса характерно равенство индуктивного и емкостного сопротивлений:

(1)

Добиться этого равенства можно изменением одной из трех величин - и .

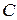Резонанс в цепи (рис.1а) возникает при

(2)

где - резонансная частота.

Рис.1

Если к цепи приложено неизменное напряжение, то в режиме резонанса ток в ней приобретает максимальное значение и становится равным:

(3)

При этом напряжения на конденсаторе и катушке :

(4)

и превышает напряжение на зажимах цепи, если и .

Отношение называется добротностью цепи. Величину d, обратную добротности, называют затуханием:

, (5)

где - волновое сопротивление цепи.

Величина добротности показывает, во сколько раз падение напряжения на индуктивности или емкости превышает напряжение, приложенное к цепи, в режиме резонанса напряжений:

. (6)

Векторная диаграмма напряжений и тока в режиме резонанса напряжений приведена на рис.1

Для изучения резонанса напряжений наибольший интерес представляют частотные зависимости , и , разности фаз приложенного напряжения и тока 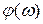. Такие кривые представлены на рис.2а. Как видно из этого рисунка, максимум имеет место при частоте, большей , а максимум - при частоте, меньшей ; расхождение будет тем больше, чем больше величина затухания. При изменении частоты от 0 до реактивное сопротивление цепи (рис.2б) имеет емкостной характер и изменяется от до 0. При этом ток возрастает от нуля до наибольшего значения , а угол сдвига фаз между током и напряжением изменяется от до . При изменении частоты от до результирующее реактивное сопротивление возрастает от 0 до и имеет уже индуктивный характер. При этом ток уменьшается от наибольшего значения до нуля, а угол возрастает от 0 до .

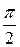Влияние параметров цепи на вид резонансных кривых можно учитывать, используя величину добротности .

В самом деле, комплекс полного сопротивления цепи (рис.1) равен:

В результате несложных преобразований получим:

. (7)

Следовательно, частотная характеристика модуля полного тока определяется уравнением:

. (8)

Для удобства сравнения частотных характеристик цепей с различной величиной добротности рассматривают зависимости:

(9)

На рис.2а кривые имеют большее значение Q, чем кривая I.

Используя кривые рис.2а, легко определить добротность или затухание цепи. Для этого на высоте проводят прямую, параллельную оси абсцисс. Тогда:

. (10)

После несложных преобразований получим:

.

Считая, что , последнее выражение приведем к виду:

,

учитывая, что , откуда

, (11)

где - резонансная частота;

- зона частот, называемая полосой пропускания при крайних частотах и и токе .

Используя величину добротности, определенную на основании графических зависимостей, легко найти активное сопротивление цепи.

Резонансные методы часто используются для измерения параметров цепи. Так, например, можно определить индуктивность и активное сопротивление катушки индуктивности по схеме рис.3

Последовательно с исследуемой катушкой включаем известные по величине емкость С и измерительное сопротивление 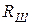. Изменяя частоту генератора, добиваемся в цепи резонанса при . В случае резонанса входное сопротивление будет чисто активным и тогда:

(12)

Измерив, входное напряжение и напряжение на известном 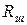, можем вычислить активное сопротивление катушки из (12)

(13)

Индуктивность катушки можно определить из выражения для резонансной частоты:

,

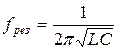откуда

. (14)

Поиск по сайту: