Основные теоретические положения

3.1. Явление взаимной индукции.

Взаимной индукцией называется явление наведения ЭДС в одном из участков электрической цепи вследствие изменения тока, протекающего по другому участку.

Потокосцепление взаимной индукции:

где - поток взаимной индукции в 1 катушке, обусловленный потоком второй катушки;

- поток взаимной индукции во 2 катушке, обусловленный током первой катушки;

- токи в катушках;

- число витков катушек;

- взаимная индуктивность контуров.

Рис.1

При постоянной магнитной проницаемости среды, в которой создается магнитное поле, величина взаимной индуктивности зависит только от числа витков обеих катушек, от конструкции и взаимного расположения катушек.

Потоки самоиндукции катушек ( и ) и потоки взаимоиндукции ( и ) могут быть направлены согласно (в одну сторону) или встречно (в противоположные стороны).

Поэтому различают согласное и встречное включение индуктивно-связанных катушек.

При согласном включении полная ЭДС первой катушки равна:

При встречном включении имеем:

Или в комплексной форме:

.

Часто в уравнениях цепи вместо ЭДС индукции записывают напряжения, уравновешивающие эти ЭДС:

; .

Тогда уравнения (6) можно переписать в виде:

.

Если собственная индуктивность всегда положительная, то взаимная индуктивность может быть как положительной, так и отрицательной.

Связь между двумя катушками с собственными индуктивностями и и взаимной индуктивностью характеризуется коэффициентом связи:

причем

На схемах электрических цепей принято обозначать (маркировать) начала обмоток определенным значком, например звездочкой (*).

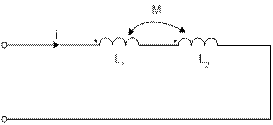
Рис.2

Тогда для учета знака напряжения взаимоиндукции применяют следующее правило. Если выбранные положительные направления токов в катушках одинаково ориентированы относительно звездочек (т.е. начал обмоток), то знаки напряжений самоиндукции и взаимной индукции одинаковы, если нет – знаки противоположны.

Рис.3

Примечание: В этом случае взаимоиндуктивность должна быть задана по величине и знаку.

3.2. Последовательное соединение индуктивно-связанных катушек:

Рис.4

Для схемы рис.4 имеем одинаковую ориентацию токов относительно звездочек, т.е. согласное включение:

.

Отсюда эквивалентные сопротивления последовательной цепи

На основании выражений (12), (13) и (14) легко установить, что при согласном включении катушек, индуктивная связь увеличивает эквивалентные реактивные сопротивления обеих катушек и всей цепи в целом, а при встречном включении, наоборот, уменьшает.

Представляет интерес случай, когда . Тогда эквивалентное индуктивное сопротивление катушки . А это формально означает, что вторая катушка эквивалентна некоторой емкости. Это явление называется эффектом ложной емкости.

3.3. Параллельное соединение индуктивно-связанных катушек.

Рис.5

Для параллельного соединения справедливы следующие соотношения:

где знак «+» относится к согласному включению, а знак «-«к встречному включению.

Обозначив , и и решая (15) относительно токов, получим

;

.

Отсюда определим выражения для эквивалентных комплексных сопротивлений обеих ветвей и всей цепи в целом:

;

;

где в знаменателе знак «-» соответствует согласному включению, а знак «+» - встречному.

Составим выражение для баланса мощностей. Комплексные мощности первой и второй катушек определяются таким образом:

.

В выражении (18) и комплексные выражения полной мощности, передаваемой индуктивным путем из первой катушки во вторую и из второй в первую.

Записав выражения для токов в виде: и

Получим

Отсюда следует, что:

Из этих выражений видно, что в общем случае полные мощности, соответствующие потоку взаимной индуктивности катушек, имеют активные и реактивные составляющие. Их величина и знак зависят от схемы включения и параметров катушек. Что касается активных мощностей, то из (20) следует, что

,

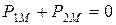т.е. путем взаимной индукции происходит односторонняя передача активной мощности из одной катушки в другую.

Для получения баланса мощностей подставим (19) в (18):

.

и - суммарные активные мощности обеих катушек, они могут быть обе положительными или одна - отрицательная, но их сумма всегда положительна.

и - суммарные реактивные мощности обеих катушек.

и - активные мощности, выделяемые в катушках в виде тепла.

и - активные мощности, передаваемые катушками друг другу посредством потока взаимной индукции.

и - реактивные мощности обеих катушек, обусловленные их потоками самоиндукции.

Рассмотрим баланс активных мощностей в двух частных случаях.

3.3.1. Соединение встречное.

.

,

т.е. сеть доставляет мощность , расходуемую в первой катушке, за вычетом мощность передаваемой из второй катушки в первую.

,

т.е. сеть доставляет во вторую катушку мощность , расходуемую во второй катушке на нагрев, и мощность Р, которая передается из второй катушки в первую.

3.3.2. Соединение согласное

.

Из (20) получаем:

; .

Значит мощность передается из первой катушки во вторую:

.

3.4. Экспериментальное определение взаимной индуктивности.

Взаимную индуктивность можно определять двумя способами:

3.4.1. По величине ЭДС взаимной индукции. Для определения М используется соотношение:

где (или ) напряжение на разомкнутых концах второй (или первой) катушки при протекании тока 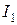в первой или тока во второй катушке.

3.4.2. Последовательным соединением при согласном и встречном включении катушек.

Тогда для согласного включения: ,

для встречного .

Вычитая одно равенство из другого получаем выражение для :

.

Поиск по сайту: