Основные теоретические положения. Если задана некоторая схема и требуется найти ток в одной ее ветви, то мысленно заключим всю схему, содержащую источники и сопротивления в прямоугольник

Если задана некоторая схема и требуется найти ток в одной ее ветви, то мысленно заключим всю схему, содержащую источники и сопротивления в прямоугольник, выделив из нее одну ветвь ab, в которой требуется найти ток (рис.1а).

Ток не изменится, если в ветвь ab включить две равные и противоположнонаправленные ЭДС и 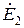(рис.1б).

На основании принципа наложения:

.

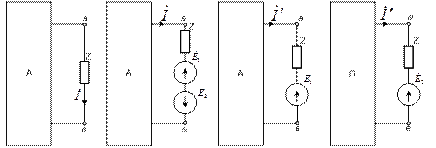
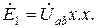
Рис.1

Пусть ток вызывается всеми ЭДС активного двухполюсника (А) и ЭДС , а ток вызывается только ЭДС 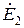, т.е. в прямоугольнике П отсутствуют вся ЭДС, но оставлены внутренние сопротивления источников.

Для схемы (рис.1в):

.

Выберем так, чтобы 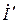был равен нулю, что соответствует размыканию ветви ab (холостому ходу). Следовательно, если выбрать 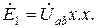, то . Тогда . Но в соответствии со схемой (рис.1г):

,

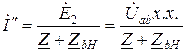где - напряжение на зажимах ab при холостом ходе;

- входное сопротивление двухполюсника по отношению к зажимам

ab;

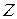- сопротивление ветви ab.

Полученному уравнению для отвечает эквивалентная схема (рис.2а), где вместо двухполюсника изображены источник ЭДС и сопротивления , которые можно рассматривать как некоторый эквивалентный генератор ( - является его внутренним сопротивление, а - его ЭДС).

Эту схему можно привести и к эквивалентному источнику тока (рис.2б).

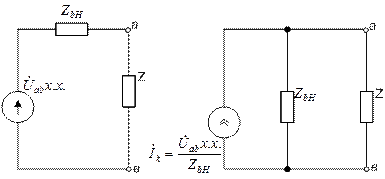
Рис.2

Поиск по сайту: