 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
При исследовании процессов»
Цель занятия: закрепление и углубление знаний по использованию методов анализа в исследовании социально-экономических процессов; приобретение навыков применения метода вариационного факторного анализа; показ возможности и необходимости использования методов исследования, выработанных другими научными дисциплинами, в частности статистикой, и относящихся к методологическому аппарату этих дисциплин, к исследованию социально-экономических процессов.
Общие положения
Вариационный анализ – частно-научный метод исследования, выработанный статистикой и относящийся к методологической базе этой науки. Он применяется при исследовании таких процессов (явлений), информация о которых носит не количественный, а качественный характер типа: да, нет; хорошо, удовлетворительно, плохо.
Метод имеет два подвида, один из которых применяется для анализа явлений, качественные признаки которых имеют дуальную классификацию (два оценочных уровня). Другой – для анализа явлений, качественные признаки которых имеют более чем два уровня дифференциации.
Для выявления наличия связи между двумя качественными признаками явления, если каждый из этих признаков оценивается двумя уровнями, определяют значения коэффициентов ассоциации (Ка) или контингентизации (Кк) в долях единицы:
Ka = 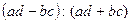 (2.1)
(2.1)
Kk = 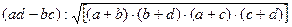 (2.2)
(2.2)
где a и b – количества наблюдений проявления исследуемого явления по первому и второму уровням дифференциации одного качественно оцененного признака, при первом уровне второго качественно оцененного признака единиц; с и d – количества наблюдений проявления того же явления по тем же первому и второму уровням одного качественно оцененного признака при втором уровне второго качественно оцененного признака.
Пример. Необходимо выявить существует ли связь между поселенческим происхождением индивида (родился в селе или в городе, уровни дифференциации первого признака) и его склонностью к наркомании (наркоман или не пользуется наркотиками, уровни дифференциации второго признака). Эта не полностью метрическая информация в совокупности с количеством наблюдений, применительно к обозначениям формул 2.1 и 2.2 может быть представлена в табличной форме.
Таблица 2.1 – Исходная информация для вариационного анализа (выявление наличия связи между двумя качественно оцененными признаками исследуемого явления при двух уровнях дифференциации этих признаков)
| Селянин | Горожанин | ||
| наркоман | не склонен | наркоман | не склонен |
| а = 95 | b = 138 | с= 147 | d= 153 |
Связь между рассматриваемыми качественно оцененными признаками считается имеющей место при значениях Ка ≥ 0,5 и Кк ≥ 0,3.
Для определения наличия связи между двумя качественно оцененными признаками явления, если каждый из этих признаков характеризуется более чем двумя уровнями дифференциации, рассчитываются значения коэффициентов взаимной сопряженности Пирсона (Кп) или Чупрова (Кч)[10]. В долях единицы:
Кп = 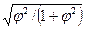 ; (2.3)
; (2.3)
Кч =  , (2.4)
, (2.4)
где φ2 – показатель взаимной сопряженности, единицы;
К1(х) и К2(у) – числа уровней проявления дифференциации каждого качественно оцениваемого признака, единицы.
Значения  и
и  , в свою очередь, определяются:
, в свою очередь, определяются:
φ2 = ∑x∑y[n2xy/(nx∙ny)/nx] – 1; (2.5)
1+φ2 = ∑x∑y[∑x∑y(n2xy/nx)/ny] = ∑x∑y[∑x∑y(n2xy/nx)/nx], (2.6)
где nху – количество проявлений (наблюдений) определенного уровня одного свойства при определенном уровне другого, единиц;
nх и ny – общие количества проявлений одного из свойств на его определенном уровне дифференциации, единиц;
n = ∑x∑ynxy – общее количество проявлений обоих свойств единиц.
Рассматриваемый подвид вариационного анализа может, таким образом, выполняться также двумя различными методами.
Пример. Необходимо выявить, существует ли связь между накладными расходами (свойство х) и себестоимостью продукции[11] (свойство у), при фиксировании проявления каждого из этих свойств на трех качественных уровнях дифференциации: низкий, средний и высокий (Кх=3; Ку=3). Это не полностью метрическая информация; в совокупности с количеством наблюдений, применительно к обозначениям формул 3-6 может быть представлена в табличной форме (таблица 2.2).
Связь между рассматриваемыми качественно оцененными признаками, считается, имеет место при значениях Кп > 0,40, Кк > 0,3. При этих значениях связь рассматривается средней.
Таблица 2.2 – Исходная информация для вариационного анализа (выявление наличия связи между двумя качественно оцененными признаками исследуемого явления при более чем двух уровнях дифференциации этих признаков)
| Накладные расходы (признак х) | Себестоимость продукции (признак у) | Итого | |||
| уровни признака (К2 = KY = 3) | |||||
| низкий | средний | высокий | |||
| Уровни признака (К,=КХ=3) | низкий | 19 (nху) | 45 (nх) | ||
| средний | |||||
| высокий | |||||
| Итого: | 35 (nу) | 150 (n) |
Поиск по сайту: