 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Груз D массой m, получив в точке А начальную скорость v0, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис.4, табл. 4).
На участке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рисунках).
В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует переменная сила F, проекция которой Fx на ось х задана в таблице.
Считая груз материальной точкой и зная время t1 движения груза от точки А до точки В, найти скорость груза на участке ВС через t2= 2 сек после выхода из точки В. Трением груза о трубу пренебречь.



Рис.4
Таблица 4
| Номер | m, кг | v0, м/с | Q, H | t1, c | Fx, H | |
| условия | ||||||
| 2.4 | 1.5 | 2t | ||||
| 2.5 | 2t2 | |||||
| 3t2-1 | ||||||
| 1.8 | 2t2+1 | |||||
| t3 | ||||||
| 4.5 | t3+2t | |||||
| 2.5 | 2t2-1 | |||||
| 1.6 | 3t | |||||
| 4.8 | 3t2 | |||||
| 2t2-1 |
Указания. Задача Д1 - на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение точки (груза) на участке АВ, учтя начальные условия. Затем, зная время движения груза на участке АВ или длину этого участка, определить скорость груза в точке В. Эта скорость будет начальной для движения груза на участке ВС. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и полагая в этот момент t = 0.
Пример Д1. На вертикальном участке АВ трубы (рис.5) на груз D массой m действуют сила тяжести и постоянная сила Q; время движения на участке АВ t1, скорость в точке А V0 На наклонном участке ВС на груз действуют сила тяжести и переменная сила F = F(t), заданная в ньютонах.

 Дано: m = 2 кг, Q=4 Н
Дано: m = 2 кг, Q=4 Н
v0 = 5 м/с, t1 = 2,5 с, Fx = t2+1.
Определить: v2 -скорость движения груза на участке ВС через t2= 2 с после выхода из точки В..
Решение. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы P = mg и R. Проводим ось АZ и составляем дифференциальное уравнение движения груза в проекции на эту ось:
 или (1)
или (1)
Далее находим: PZ = P = mg, Учтя, что vz = v, получим
 (2)
(2)
Разделяя в уравнении (2) переменные, а затем беря от обеих частей интегралы, получим
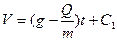 .
.
По начальным условиям при t= 0 v = v0, что дает С1 = 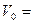 5м/с.
5м/с.
В результате находим
 (3)
(3)
Полагая в равенстве (3) t = 2.5 м, определим скорость vB груза в точке В:
 = 25 м/с.
= 25 м/с.
Теперь рассмотрим движение груза на участке ВС; найденная скорость vB будет для движения на этом участке начальной скоростью (v0 = vB). Изображаем груз (в произвольном положении) и действующие на него силы P = mg, N и F.
Проведем из точки В ось ВХ и составим дифференциальное уравнение движения груза в проекции на эту ось:
 . (4)
. (4)
Так как Рх = Psin30° = 0.5 mg, Nx = 0, Fx = t2+1, то уравнение (4) примет вид
 .
.
Разделив обе части равенства на m = 2 кг и полагая опять g @ 10 м/с2 , получим
 .
.
Умножая обе части уравнения на dt и интегрируя, найдем
vx = 5,5t +0,5t3/3+ C2.
Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t = 0. Тогда при t = 0 vx = v0 = vB., Подставляя эти величины в (11), получим
С2 = vB =25 м/с.
Тогда vx = 5,5t +0,5t3/3+ 25.
Подставляя время движения на участке ВС t2=2c находим
vx = 5,5.2 +0,5 . 23/3+ 25=37,3 м/с.
Контрольные вопросы
1. Как формулируется первый закон динамики?
2. Как формулируется второй закон динамики?
3. Как формулируется третий закон динамики?
4. Как записываются дифференциальные уравнения движения точки в декартовой системе координат?
5. Для чего нужны начальные условия?
6. Как формулируются задачи динамики?
7. Как связаны вес и масса тела?
8. Какие единицы являются основными в системе СИ?
9. В каких единицах выражается сила в системе СИ?
10. Что такое ускорение свободного падения?
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. Методические указания к выполнению контрольных работ и задания по технической механике для студентов специальностей НДб
Подписано в печать________2013. Формат 60×90 1/16. Усл. печ. л.__1___ Тираж экз. Заказ №_______
Издательство федерального государственного бюджетного
образовательного учреждения высшего профессионального образования
«Тюменский государственный нефтегазовый университет»
625000, г. Тюмень, ул. Володарского, 38.
Отдел оперативной полиграфии издательства.
625039, Тюмень, ул. Киевская, 52.
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Методическое пособие
для студентов заочной формы обучения
Издание второе, исправленное и дополненное
Направления (специальности):
141100.62 Энергетическое машиностроение
150700.62 Машиностроение
151000.62 Технологические машины и оборудование
151900.62 Конструкторско-технологическое обеспечение машиностроительных производств
160700.62 Двигатели летательных аппаратов
160700.65 Проектирование авиационных и ракетных двигателей
Поиск по сайту: