Задача Д3

(тема: “Теорема об изменении кинетической энергии системы”)

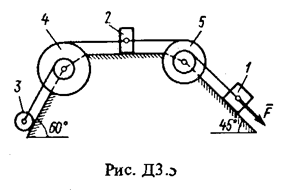
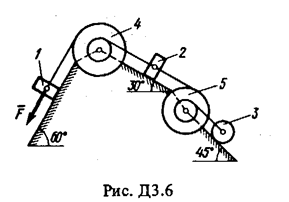
Механическая система состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость f = 0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R ₄ = 0,3 м, r ₄ = 0,1 м, R ₅ = 0,2 м, r ₅ = 0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу) (рис. Д3.0 – Д3.9, табл. Д3). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям.

Под действием силы F = f (s), зависящей от перемещения точки при­ложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивлений, равные соответственно M ₄ и М ₅.

Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы равно s,. Искомая величина указана в столбце "Найти" таблицы, где обозначено: - скорость груза 1, - скорость центра масс катка 3, - угловая скорость тела 4 и т.д.

Таблица Д3

Номер усло-вия	m 1, кг	m2, кг	m 3, кг	m 4, кг	m 5, кг	M 4, Н×м	M 5, Н×м	F = f(s)	s 1, м	Найти
							0,8	50(2+3 s)	1,0
						0,6		20(5+2 s)	1,2
							0,4	80(3+4 s)	0,8
						0,3		40(4+5 s)	0,6
							0,6	30(3+2 s)	1,4
						0,9		40(3+5 s)	1,6
							0,8	60(2+5 s)	1,0
						0,6		30(8+3 s)	0,8
						0,3		40(2+5 s)	1,6
							0,4	50(3+2 s)	1,4

Теорема об изменении кинетической энергии механической системы (краткие сведения из теории) Кинетическая энергия.Кинетической энергией точки называется величина , где m – масса точки, – абсолютная скорость точки. Кинетическая энергия механической системы , (1) где – масса точки системы, – абсолютная скорость этой точки. При поступательном движении твердого тела 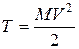, где M – масса тела, – скорость тела; при вращении твердого тела вокруг неподвижной оси , где – момент инерции тела относительно оси вращения, w – угловая скорость тела; при плоском движении тела , где M – масса тела, – скорость центра масс, – момент инерции тела относительно оси, проходящей через центр масс С, w – угловая скорость тела.

Момент инерции тела относительно оси z – это величина , где – масса точки тела, – расстояние от этой точки до оси z. Момент инерции тела зависит от формы тела и положения оси z. Значения для однородных тел простой формы (кольцо, стержень, диск, прямоугольник, цилиндр и т. д.) приводятся в справочниках по механике; значения , необходимые для решения данной задачи, приведены ниже в указаниях к решению. Если задан радиус инерции r тела, то 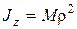, где M – масса тела. Элементарная работа силы dA на бесконечно малом перемещении ds точки, в которой приложена сила, равна , (2) где 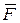– сила, ds – модуль бесконечно малого перемещения точки, – скорость точки, в которой приложена сила (направление совпадает с направлением ). Выражение (2) – одна из возможных форм записи . Например, если учесть, что , то из (2) следует еще одна форма записи: , (3) где dt – время бесконечно малого перемещения. Из (2) (или (3)) следует, что если ; если ; если ; если . Если сила приложена к точке вращающегося тела, то, применяя (2), получим , (4) где – момент силы относительно оси вращения тела, – бесконечно малый угол поворота тела. Если на тело действует пара сил, то (4) дает элементарную работу пары сил, где – момент пары сил относительно оси z. Работа силы на конечном перемещении точки из в 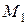. (5) Из (5) следуют выражения для работы силы в частных случаях. Работа силы тяжести (постоянной): , где P=mg – сила тяжести, – перемещение центра масс тела по вертикали. Знак “–“ соответствует движению центра масс вверх.

Теорема об изменении кинетической энергии системы. Формулировка (в интегральной (конечной) форме): изменение кинетической энергии системы на некотором конечном перемещении системы из одного положения в другое равно сумме работ всех внешних и внутренних сил, приложенных к точкам системы на соответствующих конечных перемещениях точек приложения этих сил. Математическая запись: . Если система состоит из абсолютно твердых тел, соединенных нерастяжимыми нитями или стержнями (неизменяемая система), то .

Указания. Задача ДЗ - на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел: эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении кинетической энергии катка, совершающего плоское движение, для установления зависимости между его угловой скоростью и скоростью его центра масс воспользоваться понятием о мгновенном центре скоростей (кинематика). При определении работы все перемещения следует выразить через заданное перемещение s ₁, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.

Когда по данным таблицы m ₂ = 0, груз 2 на чертеже не изображать; шкивы 4 и 5 всегда входят в систему.

Пример ДЗ. Механическая система (рис. ДЗ) состоит из сплошного цилиндрического катка l, ступенчатого шкива 2 с радиусами ступеней R ₂ и r ₂ (масса шкива равномерно распределена по его внешнему ободу) и груза 3 (коэффициент трения груза о плоскость равен f). Тела системы соединены друг с другом нитями, намотанными на шкив 2.

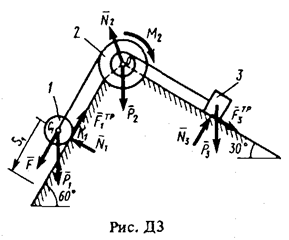
Под действием силы F = f (s), зависящей от перемещения s точки ее приложения, система приходит в движения из состояния покоя. При движении на шкив 2 действует постоянный момент М 2 сил сопротивления. Дано: m 1 = 4 кг, m 2 = 10кг, m 3 = 8 кг, R 2 = 0,2 м, r 2 = 0,1м, f = 0,2. М 2 = 0,6 Н × м, F = 2(1+2 s) Н, s 1 = 2м. Определить: скорость центра масс катка, когда s = s 1.

Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из тел 1 2, 3, соединенных нитями. Изобразим все действующие на систему внешние силы: активные , момент сопротивления М ₂ реакции и силы трения и .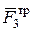

Для определения воспользуемся теоремой об изменении кинетической энергии системы

(1)

2. Определяем Т ₀ и Т. Так как в начальный момент система находилась в покое, то Т ₀ = 0. Величина Т равна сумме энергий всех тел системы:

(2)

Учитывая, что тело 1 совершает плоское движение, тело 3 движется поступательно, а тело 2 вращается вокруг неподвижной оси, получим

(3)

Все входящие сюда скорости следует выразить через искомую . Приняв во внимание, что точка K ₁ - мгновенный центр скоростей катка 1, и обозначив радиус катка через r ₁, получим

(4)

Кроме того, входящие в (3) моменты инерции имеют значения

(5)

Подставив все величины (4) и (5) в равенство (3), а затем используя равенство (2) получим окончательно:

(6)

3. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда точка С ₁ пройдет путь s ₁. Одновременно все перемещения следует выразить через заданную величину s ₁, для чего учтем, что здесь зависимость между перемещениями будет такой же, как и между соответствующими скоростями в равенствах (4), т.е. 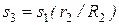. В результате получим:

Работа остальных сил равна нулю, так как точка K ₁, где приложены силы и , является мгновенным центром скоростей, точка O, где приложены , и , неподвижна, а реакция перпендикулярна перемещению груза 3. Тогда окончательно

(7)

4. Подставив выражения (6) и (7) в уравнение (1) и учитывая, что T ₀ = 0, получим

(8)

При числовых значениях заданных величин равенство (8) дает

Отсюда находим искомую скорость.

Ответ: = 1.53м/с.

Поиск по сайту: