 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача К2
(тема: “Кинематика плоского механизма”)
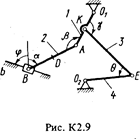
Плоский механизм состоит из стержней 1-4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О 2, шарнирами (рис. К2.0-К2.9). Длины стержней: l1 = 0,4 м, l2 = 1,2 м, l3 = 1,4 м, l4 = 0,8 м. Положение механизма определяется углами a, b, g, j, q, которые вместе с другими величинами заданы в табл. К2. Точка D на всех риcyнках и точка K на рис. К2.7-К2.9 расположены в середине соответствующего стержня.

| 
|

| 
|

| 
|

| 
|

| 
|
Определить величины, указанные в таблице в столбце "Найти". Найти также ускорение аА точки А стержня 1, если стержень 1 имеет в данный момент времени угловое ускорение ɛ 1 = 10 с-2.
Таблица К2
| Номер условия | Углы | Дано | Найти | ||||||
| a° | b° | g° | j° | q° | w 1/с | w 1/с | u м/с | ||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
| |||||||
| - | - | 
|
Дуговые стрелки на рисунках показывают, как при построении чертежа должны откладываться соответствующие углы, т.е. по ходу или против хода часовой стрелки (например, угол g на рис. 1 следует отложить от стержня DE против хода часовой стрелки, а на рис. 2 - от стержня АЕ по ходу часовой стрелки).
Построение чертежа начинать со стержня, направление которого определяется углом a; ползун В и его направляющие для большей наглядности изобразить, как в примере К2 (см. рис. К2). Заданную угловую скорость считать направленной против хода часовой стрелки, а заданную скорость uВ- от точки В к b.
Указания. Задача К2 - на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
| Теорема сложения скоростей (метод полюса) | |||

| Абсолютная скорость 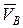 любой точки B тела равна векторной сумме скорости любой точки B тела равна векторной сумме скорости 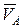 полюса и скорости полюса и скорости  точки B в относительном движении вокруг полюса A: точки B в относительном движении вокруг полюса A:  .
Вектор .
Вектор  , модуль , модуль  . .
| ||
| Теорема о проекциях скоростей | |||

| Проекции абсолютных скоростей точек на прямую, соединяющую эти точки, алгебраически равны. . |
| Метод мгновенного центра скоростей тела (МЦС) | |
Определение: МЦС тела называется точка  подвижной плоскости, абсолютная скорость которой в данный момент времени равна нулю подвижной плоскости, абсолютная скорость которой в данный момент времени равна нулю 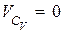 . МЦС тела находится на пересечении перпендикуляров, проведенных в двух точках тела к векторам абсолютных скоростей этих точек. . МЦС тела находится на пересечении перпендикуляров, проведенных в двух точках тела к векторам абсолютных скоростей этих точек.
| |

|
Если точку  взять за полюс, то приходим к выводу: абсолютные скорости точек тела соответствуют мгновенному повороту тела вокруг МЦС тела. взять за полюс, то приходим к выводу: абсолютные скорости точек тела соответствуют мгновенному повороту тела вокруг МЦС тела.
 , , 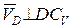 , ,  , ,  . .
|
Пример К2. Механизм (рис. К2, а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами.

Дано: a = 120°, b = 60°, g = 90°, j = 0°, q = 30°. AD = DE, l 1 = 0,6 м, l 3 = 1,2 м, w 1 = 5 с-1, ɛ 1 =8 с-2.
Определить:  и аA.
и аA.
Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. К2, б).
2. Определяем uE. Точка Е принадлежит стержню AЕ. Чтобы найти uE, надо знать скорость какой-нибудь другой точки этого стержня и направление uE. По данным задачи можем определить
 (1)
(1)
Направление  найдем, учтя, что точка Е принадлежит одновременно стержню 0 2 Е, вращающемуся вокруг О 2; следовательно,
найдем, учтя, что точка Е принадлежит одновременно стержню 0 2 Е, вращающемуся вокруг О 2; следовательно,  ^ 0 2 Е. Теперь, зная
^ 0 2 Е. Теперь, зная  и направление
и направление  , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АЕ) на прямую, соединяющую эти точки (прямая АЕ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АЕ) на прямую, соединяющую эти точки (прямая АЕ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор  (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
 (2)
(2)
3. Определяем uВ. Точка В принадлежит стержню BD. Следовательно, по аналогии с предыдущим, чтобы определить uВ, надо сначала найти скорость точки D, принадлежащей одновременно стержню АЕ. Для этого, зная  и
и  , построим мгновенный центр скоростей (МЦС) стержня АЕ; это точка С 2, лежащая на пересечении перпендикуляров к
, построим мгновенный центр скоростей (МЦС) стержня АЕ; это точка С 2, лежащая на пересечении перпендикуляров к  и
и  , восставленных из точек А и Е (к
, восставленных из точек А и Е (к  и
и  перпендикулярны стержни 1 и 4).По направлению вектора
перпендикулярны стержни 1 и 4).По направлению вектора  определяем направление поворота стержня АЕ вокруг МЦС С 2. Вектор
определяем направление поворота стержня АЕ вокруг МЦС С 2. Вектор  будет перпендикулярен отрезку С 2 D, соединяющему точки D и С 2, и направлен в сторону поворота. Величину
будет перпендикулярен отрезку С 2 D, соединяющему точки D и С 2, и направлен в сторону поворота. Величину  найдем из пропорции
найдем из пропорции
 (3)
(3)
Чтобы вычислить С 2 D и С 2 А, заметим, что D AС 2 E - прямоугольный, так как острые углы в нем равны 30 и 60°, и что С 2 А = AE sin 30° = 0,5 АЕ = AD. Тогда D AС 2 D является равносторонними С 2 А = С 2 D. В результате равенство (3) дает
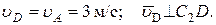 (4)
(4)
Так как точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно, то направление  известно. Тогда, восставляяиз точек В и D перпендикуляры к скоростям
известно. Тогда, восставляяиз точек В и D перпендикуляры к скоростям  и
и  , построим МЦС С 3 стержня BD. По направлению вектора
, построим МЦС С 3 стержня BD. По направлению вектора  определяем направление поворота стержня BD вокруг центра С 3. Вектор
определяем направление поворота стержня BD вокруг центра С 3. Вектор  будет направлен в сторону поворота стержня BD. Из рис. К2, б видно, что Ð С 3 DB = 30°, a Ð D С 3 B = 90°, откуда С 3 B = l 3 sin 30°, С 3 D = l 3 cos 30°. Составив теперь пропорцию, найдем, что
будет направлен в сторону поворота стержня BD. Из рис. К2, б видно, что Ð С 3 DB = 30°, a Ð D С 3 B = 90°, откуда С 3 B = l 3 sin 30°, С 3 D = l 3 cos 30°. Составив теперь пропорцию, найдем, что

 (5)
(5)
4. Определяем w3. Так как МЦС стержня 3 известен (точка С3), то

5. Определяем аA. Так как ɛ 1 известно, то аAt=l 1 ɛ 1. Далее  , или
, или  . Тогда
. Тогда  . Произведя вычисления, получим аА = 15,8 м/с2.
. Произведя вычисления, получим аА = 15,8 м/с2.
Ответ: uЕ = 5,2 м/с, uВ = 1,7 м/с, w3 = 2,9 с-1, аА = 15,8 /с2.
Поиск по сайту: