 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение. 1. Строим положение механизма в соответствии с заданными углами (рис
1. Строим положение механизма в соответствии с заданными углами (рис. Д4б); при этом, согласно указанию к задаче Д4, прикрепляем пружину к ползуну с другой стороны (так, как если бы было 
).
Система состоит из стержней 1, 2, 3 и ползунов B, D; система имеет одну степень свободы.
Применим принцип возможных перемещений:
,
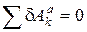или
(1)
(так как в задаче К4 мы уже встречались с определением скоростей точек плоского механизма).
2. Покажем на рисунке действующие на точки механизма активные силы: силу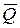 
, силу упругости 
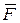пружины (предполагая, что пружина растянута) и пару с моментом М.
Неизвестную силу F найдем с помощью уравнения (1), а зная F и учитывая, что 
, определим l.
3. Сообщим системе возможное перемещение. При этом стержень 1 приобретет угловую скорость w1, ползун B – скорость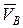 
, ползун D – скорость 
; эти скорости потребуются при вычислении слагаемых в (1). Так как система имеет одну степень свободы, то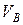 
и 
можно выразить через w1. Ход расчетов такой же, как в задаче К4.
4. Кинематическая часть задачи. Все вычисления и построения векторов проводятся для заданного положения механизма (механизм не перемещается в новое положение), так как возможные перемещения – бесконечно малые.
Сначала найдем и изобразим на рисунке скорость точки A (направление вектора скорости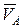 
определяется направлением угловой скорости 
):
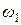Определим и изобразим на рисунке скорость точки D. Скорость – вдоль направляющих ползуна D. По теореме о проекциях скоростей точек абсолютно твердого тела, проекции скоростей и 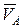на прямую AD алгебраически равны (имеют одинаковые модули и знаки):
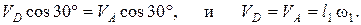(2)
Чтобы определить скорость точки 
, найдем сначала скорость точки 
. Для этого построим мгновенный центр скоростей С 2стержня 2. Он находится на пересечении перпендикуляров к векторам 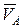и , восставленных из точек А и D. Покажем направление мгновенного поворота стержня 2 (вокруг С 2),учитывая направление 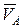или . Так как 
, то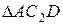 
– равносторонний и С 2 Е в нем высота, поскольку АЕ = ED. Тогда скорость 
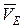, перпендикулярная С 2 Е,будет направлена по прямой ЕА (при изображении 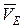учитываем направление мгновенного поворота стержня 2).
Воспользовавшись опять теоремой о проекциях скоростей точек E и A на прямую EA, получим
Значение скорости 
можно найти и другим способом, составив пропорцию
.
Находим 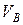, применив еще раз теорему о проекциях скоросте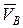й и 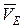на прямую BE и учитывая, что 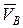параллельна направляющим ползуна B.
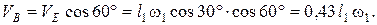
(3)
Изображаем 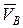на рисунке.
5. Составим уравнение (1) для показанных на рисунке сил и скоростей.
Мощность силы :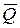 
.
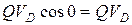Мощность силы :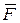 
.
Мощность пары сил: 
, так как элементарная работа пары (см. задачу Д4) 
, а мощность равна 
.
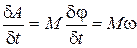В итоге, уравнение (1) принимает вид
.
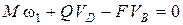Заменяя здесь и 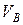их значениями (2) и (3) и вынося 
за скобки, получаем
(4)
Так как равенство (4) выполняется при любой возможной угловой скорости w1, то
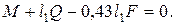(5)
Из уравнения (5) находим значение силы упругости 
и определяем деформацию пружины 
.
Ответ: l = 13,5 см. Знак указывает, что пружина, как и предполагалось, растянута.
Поиск по сайту: