АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача Д4

Читайте также:
  1. VI. Общая задача чистого разума
  2. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  3. Глава 10 Системный подход к задачам управления. Управленческие решения
  4. ГЛАВА 2.1. ЗАЩИТА ИННОВАЦИЙ КАК ЗАДАЧА УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ПРОЦЕССАМИ
  5. Глава 4. Математические основы оптимального управления в экономических задачах массового обслуживания
  6. Двойственная задача линейного программирования.
  7. Доклад о задачах власти Советов
  8. Доклад об экономическом положении рабочих Петрограда и задачах рабочего класса на заседании рабочей секции Петроградского совета рабочих и солдатских депутатов
  9. Задача 1
  10. Задача 1
  11. Задача 1
  12. ЗАДАЧА 1

(тема: “Принцип возможных перемещений”)

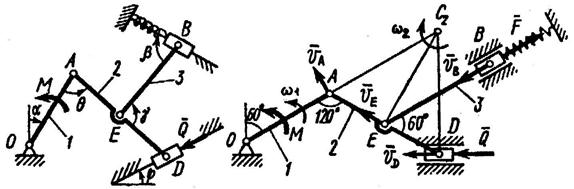
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами , , , , (рис. Д4.0-Д4.9, табл. Д4а и Д4б). Длины стержней механизма (кривошипов) равны: l 1 = 0,4 м, l 4 = 0,6 м (размеры l 2 и l 3 произвольны); точка E находится в середине соответствующего стержня.

На ползун В механизма действует сила упругости пружины ;численно 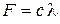, где с – коэффициент жесткости пружины, 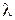– ее деформация. Кроме того, на рис. Д4.0 и Д4.1 на ползун D действует сила 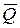, а на кривошип О 1 А – пара сил с моментом М;на рис. Д4.2- Д4.9 на кривошипы O 1 A и О 2 D действуют пары сил с моментами M 1 и М 2.

Определить, чему равна при равновесии деформация 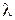пружины, и указать, растянута пружина или сжата.

Значения всех заданных величин для рис. Д4.0-Д4.4 приведены в табл. Д4а, а для рис. Д4.5-Д4.9 в табл. Д4б. В этих таблицах сила Q дана в ньютонах, а моменты М, M 1, M 2 – в ньютоно-метрах.

Построение чертежа начинать со стержня, направление которого определяется углом ; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д4 (см. рис. Д4, а также рис. Д4.10б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д4.10а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д4.10б, где одновременно иначе изображены направляющие).

Перед выполнением задания прочтите по учебнику тему: «Принцип возможных перемещений».

 

Ответьте на вопросы:

1. Как определяется число степеней свободы системы?

2. Что такое обобщенные координаты?

3. Что называется возможными перемещениями системы?

4. Формулы для вычисления элементарной работы силы на возможном перемещении (сравните с формулами, которые применили в задаче Д4).

5. Какие связи называются идеальными?

6. Сформулируйте принцип возможных перемещений для системы и запишите соответствующее уравнение.

7. Запишите уравнение мощностей, эквивалентное принципу возможных перемещений.

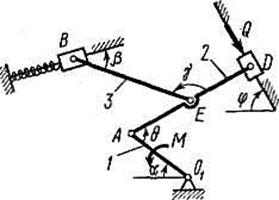Рис. Д4.0  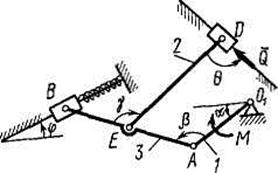 Рис. Д4.1  
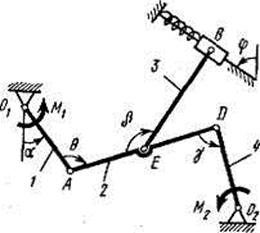Рис. Д4.2 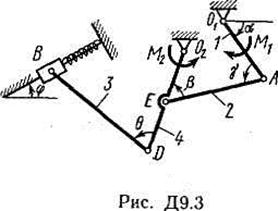Рис. Д4.3  
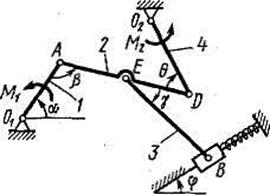Рис. Д4.4 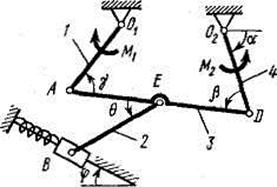Рис. Д4.5
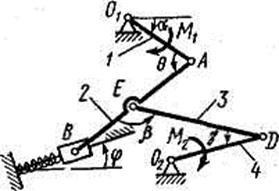Рис. Д4.6 Рис. Д4.7
 

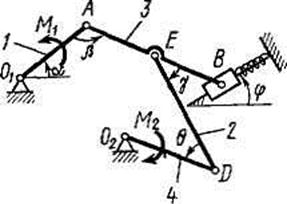
Рис. Д4.8

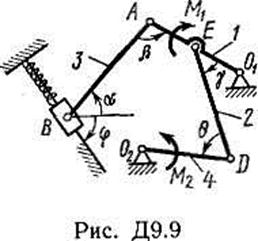 Рис. Д4.9

 

Рис. Д4.10

Таблица Д4а (к рис. Д4.0-Д4.4)

Номер условия Углы, град с, Н/см Для рис. 0-1 Для рис. 2-4
M Q M 1 M 2
                     
                     
                     
                     
                     
                     
                     
                     
                     
                     

 

 

Таблица Д4б (к рис. Д4.5-Д4.9)

Номер условия Углы, град с, Н/см M 1 M 2
                 
                 
                 
                 
                 
                 
                 
                 
                 
                 

 

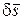Принцип возможных перемещений (краткие сведения из теории) Возможным перемещением механической системы называется совокупность а) бесконечно малых б) мысленных перемещений точек системы, при которых в) не нарушаются связи, наложенные на систему. Возможное перемещение любой точки системы будем изображать элементарным вектором , направленным в сторону перемещения. Число степеней свободы. Число независимых перемещений точек системы называется числом степеней свободы системы. Если система состоит из n точек, на которые наложены k геометрических (не накладывающих ограничений на скорости точек) связей, то она имеет степеней свободы. В дальнейшем связи считаются геометрическими. Следовательно, чтобы задать положение такой системы в любой момент времени, не нужно задавать все координаты всех точек, а надо задать только независимые параметры. Независимые параметры, число которых равно числу степеней свободы, и которые однозначно определяют положение всей системы в любой момент времени, называются обобщенными координатамии обозначаются 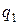, ,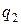…, , 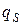где s – число степеней свободы. В качестве обобщенных координат можно выбрать декартовы координаты точек, углы поворота тел и т.д.  
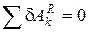Идеальные связи. Связи называются идеальными, если сумма элементарных работ реакций связей, наложенных на систему, равна нулю на любом возможном перемещении системы: . (Элементарная работа на возможном перемещении обозначается 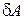). Все встречавшиеся ранее связи (шарниры, поверхности, нити, подшипники и т.д.) – идеальные при отсутствии трения. Если трение имеется и работа силы трения отлична от нуля, то сила трения включается в число активных сил. Принцип возможных перемещений. Формулировка: для равновесия системы с геометрическими идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, действующих на точки системы, на любом возможном перемещении системы из данного положения была равна нулю: 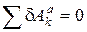, (1) или (с учетом выражений для элементарной работы силы, см. задачу Д4) 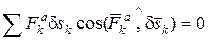, а также 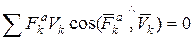. (2) В (2) выполнено деление на и поэтому суммируются мощности сил.

Указания. Задача Д4 – на применение условия равновесия механической системы – принципа возможных перемещений. Механизм в рассматриваемой задаче имеет одну степень свободы, т. е. одно независимое возможное перемещение. Для решения задачи нужно сообщить механизму возможное перемещение, вычислить сумму мощностей всех действующих активных сил и пар на этом перемещении и приравнять ее нулю. Все вошедшие в составленное уравнение скорости следует выразить через какую-либо одну из них.

Чтобы найти деформацию пружины , надо из полученного соотношения определить силу упругости F. На чертеже эту силу можно направить в любую сторону (т.е. считать пружину или растянутой, или сжатой); верно ли выбрано направление силы, укажет знак силы.

Последовательность действий при решении задачи см. в примере Д4.

Пример Д4. Механизм (рис. Д4а), расположенный в горизонтальной плоскости, состоит из стержней 1, 2, 3 и ползунов В, D, соединенных друг с другом и с неподвижной опорой О шарнирами. К ползуну В прикреплена пружина с коэффициентом жесткости с, к ползуну D приложена сила , а к стержню 1 (кривошипу) – пара сил с моментом М.

Дано: α= 60°, β = 0°, γ = 60°, φ = 0°, θ= 120°, l 1 = 0,4 м, АЕ = ED, с =125 Н/см, М = 150 H×м, Q = 350 Н.

Определить: деформацию пружины при равновесии механизма.

 

 

А) б)

Рис. Д4


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)