Дифференциальные уравнения с разделяющимися переменными

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Определение 1. Уравнение, содержащее независимую переменную, а также неизвестную функцию этой переменной и её производные или дифференциалы, называется обыкновенным дифференциальным уравнением:

F (x, y, y ¢, …, у ^(п) ) = 0. (1)

Определение 2. Порядком дифференциального уравнения называется наивысший порядок содержащихся в нём производных.

Например, x cos y + (y ¢ – y ²)sin x = 0 - уравнение первого порядка,

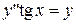- второго порядка и т.д.

Определение 3. Общим решением дифференциального уравнения п -го порядка (1) называют функцию

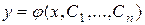, (2)

зависящую от аргумента х и п произвольных постоянных С₁,…С_п, и такую, что она при подстановке в уравнение (1) превращает его в тождество.

Если общее решение задаётся в неявной форме

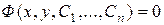, (3)

то его называют общим интегралом уравнения (1).

Определение 4. Общее решение (общий интеграл), в котором вместо произвольных С₁,…С_п подставлены конкретные числа, называется частным решением (частным интегралом).

Для нахождения значений постоянных С₁,…С_п необходимо задать п начальных условий.

Определение 5. Совместное задание дифференциального уравнения и соответствующего количества начальных данных называется задачей Коши:

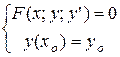
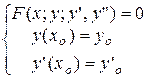(4)

Теорема (о существовании и единственности решения)

Если в дифференциальном уравнении 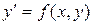функци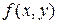и и 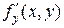непрерывны в области D, содержащей точку 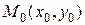, то существует единственное решение этого уравнения, удовлетворяющее условию .

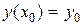Пример1.

Закон радиоактивного распада.

Известно, что скорость распада радиоактивного вещества пропорциональна его количеству. Пусть y(t) - количество вещества, .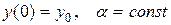

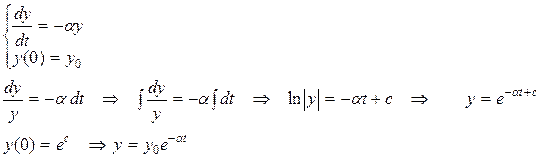
Дифференциальные уравнения с разделяющимися переменными

Определение 6. Дифференциальное уравнение первого порядка вида

N(x)dx+M(y)dy=0 (5)

называется дифференциальным уравнением с разделенными переменными.

Общий интеграл такого уравнения находится по формуле:

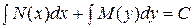(6)

Пример 2. Найти общее решение уравнения

-

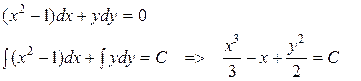-общий интеграл,

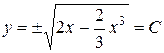- общее решение. Знак перед радикалом можно определить из начальных условий.

Определение 7. Дифференциальное уравнение первого порядка вида

P(x)R(y)dx+Q(x)S(y)dy=0 (7)

называется дифференциальным уравнением с разделяющимися переменными. Его можно привести к уравнению с разделенными переменными вида (6) путем деления обеих частей на Q(x)R(y):

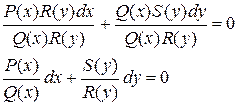
Т.е. получим уравнение с разделенными переменными, которое решается интегрированием.

Пример 3. Найти общий интеграл уравнения

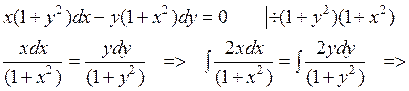
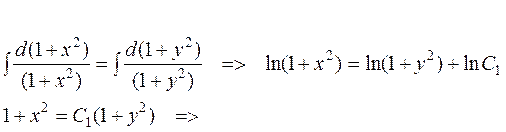
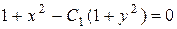- общий интеграл.

Пример 4.

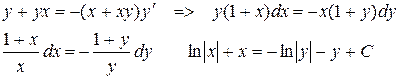
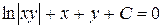- общий интеграл

Пример 5.

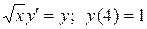- (задача Коши).

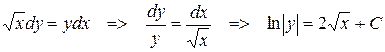- общий интеграл

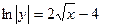- частный интеграл

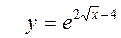- частное решение (решение задачи Коши)

Упражнения

1. Решить дифференциальные уравнения

1)	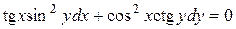;	2)	;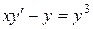
3)	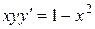;	4)	;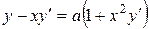
5)	;	6)	;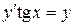
7)	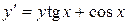;	8)	;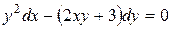
9)	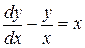;	10)	.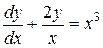
11)	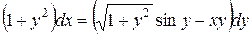;	12)	;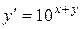
13)	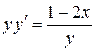;	14)	;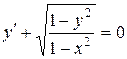

Поиск по сайту: