Понятие и теории экономического роста. Экономический рост в современной экономике

Экономический рост – это увеличение объемов созданных за определенный период времени товаров и услуг, возрастание экономического потенциала страны.

В классической теории факторам производства вменяются доли производимых ими продукта, совокупного дохода. С целью факторного анализа обеспечения экономического роста используется аппарат так называемой производственной функции:

(1)

при условии, что dF/da1, dF/dа2,..., dF/dаn представляют собой предельные производительности каждого из задействованных факторов производства. Как частный случай производственной функции можно использовать формулу Кобба — Дугласа:

(2)

где Y — национальный продукт; L — труд; К — капитал; А — постоянный коэффициент, отражающий воздействие прочих факторов (его еще называют коэффициентом пропорциональности или масштабности); A и B — переменные коэффициенты эластичности соответственно по труду и капиталу. Причем A+B = 1, или B = 1 — A; еn — фактор, отражающий влияние качественных изменений в производстве, в том числе технического прогресса.

Неоклассическая модель (Р.Солоу)

Помимо той или иной комбинации факторов производства гибкость производственной функции обеспечивают специальные коэффициенты. Их называют коэффициентами эластичности. Это степенные коэффициенты факторов производства, показывающие, как возрастёт объём продукции, если фактор производства увеличится на единицу. Коэффициент эластичности находят эмпирически, решая для этого специальную систему уравнений, полученную из исходной модели производственной функции.

Простейшая модель двухфакторная: капитал - К и труд - L.

Если коэффициенты эластичности постоянны, то функция записывается так:

,

где Y - национальный продукт;

L - труд (человекочасы или численность работников);

К - капитал всего общества (машино-часы или количество оборудования); α - коэффициент эластичности;

А -постоянный коэффициент (находится расчётным путём).

Запишем функцию производительности труда от капиталовооружённости и разделим параметры функции Y=F(K,L) на величину L, получим Y/L=F(K/L;1), или y=f (К;1), где y=Y/L -производительность общественного труда; K=K/L - объём используемого в обществе капитала, приходящегося на 1 работника.

Данная функция, по неоклассическим представлениям, должна иллюстрировать следующее: если объём используемого общественного капитала на одного рабочего возрастает, то растёт, но в меньшей степени продукт на одного рабочего (предельная производительность труда).

Графически это означает, что функция f(K) имеет первую производную, которая больше нуля f (K)>0. Вторая производная функции - f (К)<0. Это означает, что хотя функция и является положительной, она убывает по мере прироста продукта и производительности труда (рис.36.1).

Рис. Неоклассическая производственная функция

Капитал и труд вознаграждаются на основе соответствующих предельных производительных факторов. Вознаграждение капитала определяется тангенсом угла наклона к кривой f(K) в точке Р - предельная производительность капитала. Тогда WN - доля капитала в общем продукте; OW - доля заработной платы в продукте; OW - весь продукт.

Посткейнсианская модель Харрода-Домара (Рей Харрод, Евсей Домар)

Темп роста Р. Харрод назвал «гарантированным», так как он гарантирует полное использование существующих мощностей (в данном случае капитала)

,

где – коэффициент капиталоотдачи;

=Y/K – средняя производительность капитала.

,

,

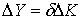
где SY - норма сбережения, предположим, величина постоянная, тогда

S=I=SY-Y, т.к. I=( Y/ ), то Y/ =SY ·Y.

Перенесём δ в правую часть и разделим обе части на Y , получим итоговую формулу

,

где Y- прирост дохода при полной занятости капиталов.

При данных темпах роста ожидания бизнесменов будут реализованы или «гарантированы». В данной модели используется производственная функция В. Леонтьева.

Перед нами график производственной функции В. Леонтьева, где MRSkl = 0 (рис).

Рис. Производственная функция В. Леонтьева

Если =1/3; Sy=0,21, то гарантирован рост на 7%. Соотношение 3:4,5 при росте Y на 1 ед.

Экономический рост в современной России имеет специфические черты, требующие особого изучения. К ним можно отнести и региональную неравномерность экономического развития, и дефицит долгосрочных инвестиций, и необходимость восстановления после длительного периода спада. Анализ экономического роста в современной России осложняется ограниченностью статистической информации, коротким периодом роста, большой долей теневой экономики.

Экономический рост на современном этапе во многом происходит благодаря процессам глобализации экономики происходящим в современном обществе. Появляются принципиально новые факторы, влияющие на него.

Поиск по сайту: