 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Существуют различные способы вычисления обобщенных сил
1. Согласно определению (2.26), обобщенная сила
Принимая во внимание, что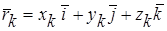 
, получаем
(2.28)
Этот способ определения обобщенных сил называют аналитическим.
Пример 2.11. Найти обобщенную силу Qq=j, если в кривошипно-ползунном механизме (рис.2.10) OA=AB= l, 
¾ вертикальная, а 
¾ горизонтальная силы.
Решение. Так как F1x=0 и F2y=0,то обобщенная сила согласно (2.28)
Проекции сил и координаты точек их приложения определяются как
F1y=- F1; F2x=- F2;
Рис.2.10 yA = l sin j; xB = 2 l cos j.
Следовательно, Qq=j = - F1 l cos j + 2 F2 l sin j.
2. Укажем на более простой способ вычисления обобщенной
силы, полезный при решении задач.
Обобщенные силы для механических систем с числом степеней свободы s=k > 1 целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит и их вариации независимы между собой. Системе всегда можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. В этом случае из (2.27)
. получаем
(2.29)
откуда 
(2.30)
Индекс qi в (2.30) означает, что виртуальная работа сил, действующих на систему, определяется на перемещениях точек приложения этих сил, соответствующих вариации только одной i– йобобщенной координаты.
Пример 2.12 Найти обобщенные силы 
и 
для системы, показанной на рис. 2.11. Масса груза (1) равна m1, массацилиндра (2)равна m2, а его радиус ¾ r. Нить по блоку (3) и цилиндру (2) не скользит. Центр масс цилиндра (2) движется вдоль вертикали.
Решение. Для определения обобщенной силы зададим приращение ds ¹ 0 координате груза (1), а для угла j поворота цилиндра (2) 
,будем считать
dj =0. При этом центр масс цилиндра (2)
будет иметь перемещение, равное перемещению груза. Следовательно,
Рис.2.11
где P1 =m1 g; P2 =m2 g.
Определяя , будем полагать, что ds=0, а dj ¹ 0. Тогда
3. Если силы, действующие на механическую систему, потенциальные, то для определения обобщенных сил можно использовать силовую функцию U или потенциальную энергию П системы.
Потенциальная сила
(2.31)
Подставляя проекции силы 
в (2.30), получаем
(2.32
Так как U = - П + const, то
(2.33)
Пример 2.13. В системе, показанной на рис. 2.12, массы груза (1) и цилиндра (2) равны m1 и m2 соответственно, радиус цилиндра (2) ¾ r, а коэффициент жесткости пружины с 1.
Полагая, что трение между грузом (1) и наклонной плоскостью отсутствует, а траектория точки С – центра масс цилиндра¾ вертикаль, найти обобщенные силы и ,
если при s =0 пружина не деформирована.
Рис. 2.12
Решение. Потенциальная энергия системы
Обобщенные силы, соответствующие обобщенным координатам:
Поиск по сайту: