 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Связи и их классификация
1. Связи называются голономными, если они описываются
уравнениями вида
(2.1)
Такие связи накладывают ограничения на координаты точек, а значит, на положение системы в пространстве. Это так называемые геометрические связи. Вместе с тем голономные связи накладывают ограничения и на скорости точек системы. Соответствующие условия получаются в результате дифференцирования уравнений (2.1) по времени:
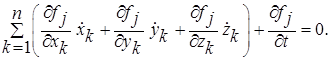(2.2)
Голономные связи могут описываться и дифференциальными уравнениями, однако последние обязательно должны быть интегрируемыми.
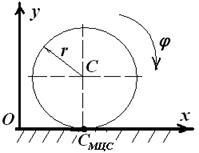Пример 2.1. Получить уравнения связей для диска радиусом r, который катится без скольжения по плоскости (рис.2.1).
Решение. Уравнения связей имеют вид
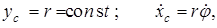
где j ¾ угол поворота диска (j = 0 при
xc = 0).
Рис.2.1 Из первого уравнения связи следует, что
Интегрируя второе уравнение, находим связь между координатой xc и углом поворота диска 
Неголономными называются связи, которые описываются уравнениями вида
(2.3)
Уравнения (2.3), в отличие от уравнений голономных связей, не
могут быть проинтегрированы независимо от дифференциальных уравнений движения системы. Неголономные связи накладывают ограничения (2.3) на скорости точек, поэтому их называют кинематическими.
Пример 2.2. Получить уравнения связей для шара радиусом r, который катится без скольжения по плоскости (рис.2.2)
Решение: Положение шара определяется координатами xc, yc, zc центра масс и тремя углами его поворота вокруг центра масс. Этими углами могут быть углы Эйлера. При любом положении шара расстояние от точки С Рис.2.2 до плоскости Оxy равно его радиусу. Поэтому одно из уравнений связи имеет вид zc = r.
Другие уравнения связи определяются из условия качения без скольжения:
где СМЦС ¾ точка соприкосновения шара с плоскостью.
Проецируя это векторное уравнение на оси неподвижной системы координат, получаем
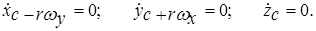
Интегрирование последнего уравнения дает полученное выше геометрическое условие zc = r.
Кинематические уравнения в проекциях на оси неподвижной системы координат имеют вид
Таким образом, уравнениями связей для шара являются
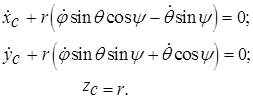
Первые два из них не интегрируются, т.е. являются уравнениями неголономных связей.
2. Связи подразделяются на стационарные и нестационарные
в зависимости от того, входит в явном виде время в уравнение связи или нет.
Связь, уравнение которой имеет вид
¾ является голономной и стационарной.
Для голономной нестационарной связи уравнение имеет вид:
Пример 2.3. Жесткий стержень длиной l, прикрепленный к неподвижной опоре и перемещающийся в плоскости xOy, (рис. 2.3)является стационарной связью для материальной точки М, находящейся на его свободном конце. Уравнения связи в декартовой системе координат, начало которой совпадает с точкой закрепления стержня, имеют вид
1. zM =0; 2. x2 + y2 - l2 =0.
Рис.2.3
Пример 2.4. Если длина стержня изменяется по заданному закону (рис. 2.4), то связь является нестационарной и уравнения связей имеют вид:
1. zM =0; 2. x2 + y2 - l2 (t) £ 0.
Р Рис.2.4
3. Связь называют удерживающей (двухсторонней), если она описывается уравнением (равенством). На рис.2.3 уравнения связи
описываются равенствами: 1. zM =0; 2. x2 + y2 - l2 =0.
В этом случае говорят, что точка во все моменты времени должна оставаться на связи.
Неудерживающая (односторонняя) связь описывается неравенством. Например, если математический маятник представляет собой тонкий стержень длиной l, вращающийся вокруг неподвижной оси и к свободному концу которого прикреплен груз (материальная точка), то связь для груза будет удерживающей. Е сли же груз прикреплен к свободному концу нерастяжимой нити длиной l, то связь будет неудерживающая, поскольку груз может находиться как на поверхности сферы радиусом l, так и внутри ее.
x2 + y2 - l2 (t) £ 0
Поиск по сайту: