АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Несвободное движение системы материальных точек

Читайте также:
  1. I. Формирование системы военной психологии в России.
  2. II. Цель и задачи государственной политики в области развития инновационной системы
  3. II. Экономические институты и системы
  4. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  5. А). Системы разомкнутые, замкнутые и комбинированные.
  6. А. И. Герцен – основатель системы вольной русской прессы в эмиграции. Литературно-публицистическое мастерство
  7. Абиотические компоненты экосистемы.
  8. Абстрактные линейные системы
  9. Автоматизированные системы контроля за исполнением документов
  10. Автоматизированные системы контроля и учета электроэнергии (АСКУЭ).
  11. Автоматизированные системы регистрации
  12. Автоматизированные системы управления (АСУ).

Рассмотрим систему, состоящую из n материальных точек, или механическую систему, положение которой определяется n точками. Положение каждой материальной точки определяется тремя координатами; положение абсолютно твердого тела – тремя точками, не лежащими на одной прямой, или шестью параметрами. Если на систему наложены связи, то координаты материальных точек и точек, определяющих положение абсолютно твердого тела, должны удовлетворять дополнительным уравнениям – уравнениям связей. Число параметров, определяющих положение абсолютно твердого тела, на которое наложены ограничения, уменьшается. Например, положение тела с одной неподвижной точкой определяется тремя углами; если у тела закреплены две точки, то его положение определяется одним углом и т.д.

Связи, наложенные на механическую систему, представляют собой некоторые материальные тела, состояние движение которых считается известным, заданным. Тела могут быть абсолютно твердыми, либо деформирующимися с известным законом изменения формы. Во всех случаях будем считать, что движение рассматриваемой механической системы не влияет на поведение связей.

Виртуальным перемещением системы называется любая совокупность виртуальных перемещений всех ее точек.

Для системы, состоящей из n точек, имеем3 n вариаций декартовых координат. Если на систему наложено h голономных удерживающих связей, то вариации координат точек системы должны удовлетворять следующим условиям:

(2.12)

Для системы с голономными связями число степеней свободы равно числу независимых обобщенных координат. В каждый момент времени положение системы может быть определено как в декартовых, так и в обобщенных координатах. Поэтому возможные и виртуальные перемещения любой точки системы выражаются через ее обобщенные координаты. Для системы с s = 3 n -h степенями свободы радиус-вектор каждой точки является функцией обобщенных координат и времени 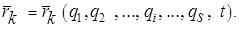Следовательно, виртуальное перемещение можно вычислить как полный дифференциал функции при фиксированном времени:

(2.13)

Таким образом,

(2.14)

где (2.15

Элементарное возможное перемещение точки определяется как полный дифференциал функции , но время при этом не фиксируется:

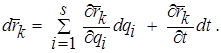(2.16)

Дальнейшая теория излагается для неизменяемой системы с голономными нестационарными удерживающими связями (2.1):

Механическая система, расстояние между точками которой в процессе ее движения не изменяется, называется неизменяемой.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)