Теоремы двойственности

1) Если одна из задач двойственной пары имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т. е. 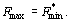Если же целевая функция одной задачи из двойственной пары неограничена сверху или снизу, то другая задача вообще не имеет планов.

2) План 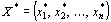исходной задачи и план двойственной задачи являются оптимальными планами этих задач тогда и только тогда, когда для любого 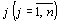выполняется равенство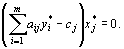

Пары двойственных задач делятся на симметричные и несимметричные. Если в системе ограничений нет ограничений вида равенства и в обеих задачах нет произвольных переменных, то такая пара называется симметричной. В противном случае – несимметричной.

25. ТЗ. В общем случае имеется m пунктов производства и n пунктов потребления. Пункты производства пронумеруем числами от 1 до m. Номер пункта производства будем обозначать буквой i (таким образом, 1 i m). Пункты потребления пронумеруем числами от 1 до n. Номер пункта потребления будем обозначать буквой j (таким образом, 1 j n). Рассмотрим некоторый период времени. Пусть ai - объем производства за период времени в i-м пункте производства, bi - количество продукции, требуемое за период времени в j-м пункте потребления. Пусть cij - стоимость перевозки единицы груза из i-го пункта производства в j-й пункт потребления.

Требуется определить план перевозок, удовлетворяющий условиям по пунктам производства и потребления и соответствующий наименьшим затратам на перевозки.

Для построения математической модели следует ввести переменные. Для каждой пары поставщик-потребитель, то есть для каждой пары (i,j) введем переменную хij - объем перевозки от пункта производства i к пункту потребления j.

Математическая модель транспортной задачи записывается следующим образом:

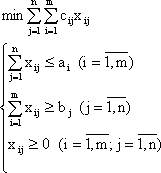
Целевая функция модели представляет собой общую стоимость всех перевозок. В модели указано, что целевую функцию следует минимизировать. Таким образом, модель предписывает искать план перевозок наименьшей общей стоимости.

В системе ограничений представлены три группы неравенств. В первой группе m неравенств, соответствующих пунктам производства. Каждое неравенство утверждает, что из соответствующего пункта не может быть вывезено больше, чем в нем имеется. Во второй группе n неравенств, соответствующих пунктам потребления. Каждое из них требует, чтобы в соответствующий пункт было привезено не меньше, чем требуется. В третьей группе m ´ n неравенств, обеспечивающих неотрицательность объема перевозок.

Представленная модель транспортной задачи с ограничениями-неравенствами называется открытой моделью. Задача разрешима в том и только в том случае, когда общий объем груза у поставщиков не меньше суммарной потребности потребителей, то есть когда выполнено неравенство: 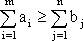. Если общий объем груза у поставщиков в точности равен общей потребности потребителей, то есть если имеет место равенство: 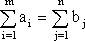, то указанная выше открытая модель эквивалентна более простой закрытой модели, в которой основные неравенства заменены равенствами. Закрытая модель имеет следующий вид:

26-27. Теорема о разрешимости транспортной задачи. Доказательство ограниченности функции на множестве планов транспортной задачи.

Теорема

Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы грузов в пунктах отправления были бы равны потребностям в грузах в пунктах потребления

m n ── ──

∑ ai = ∑ bi, i=1,m, j=1,n (1)

i=1 j=1

Для доказательства теоремы необходимо показать, что при заданных условиях существует хотя бы один план задачи и линейная функция на множестве планов ограничена.

Пусть выполняется условие

m n ── ──

∑ ai = ∑ bi = M>0, i=1,m, j=1,n

i=1 j=1,

тогда величины

aibi ── ──

xij= ── (i=1,m, j=1,n)

M

являются планом, так как они удовлетворяют системе ограничений

n

∑ xij=ai, (2)

j=1

m ── ──

∑ xij=bi, (3), i=1,m, j=1,n

i=1

Действительно, подставляя значения xij в 2 и 3, находим

n n aibi ai n ai

∑ xij=∑ ── = ─ ∑bj = ─ M = ai,

j=1 j=1 M M j=1 M

m m aibi bi m bi

∑ xij=∑ ── = ─ ∑ai = ─ M = bi

i=1 i=1 M M i=1 M

Выберем из значений Cij наибольшее C*=maxCij и заменим в линейной функции

m n

Z=∑ ∑ Cij xij все коэффициенты на на С*. Тогда, учитывая 2, получим

i=1 j=1

m n m n m

∑ ∑ = Cij xij <=C*, ∑ ∑ xij=C*, ∑ ai=C*M

i=1j=1 i=1j=1 i=1

Выберем из значений Сij наименьшее С**=minСij, и заменим в линейной функции все коэффициенты на С**, тогда, учитывая 2, имеем

m n m n m

∑ ∑ = Cij xij <=C**, ∑ ∑ xij=C**, ∑ ai=C**M

i=1j=1 i=1j=1 i=1

Объединяя два последних неравенства в одно двойное, окончательно получаем

С**<=Z<=С*М,

т.е. линейная функция ограничена на множестве планов транспортной задачи.

Поиск по сайту: