 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Цена игры. Седловые точки
Если α=β=V, то V называется ценой игры. Игра, в которой α= β, называется игрой с седловой точкой. Для игры с седловой точкой нахождение решения состоит в выборе максиминной и минимаксной стратегий, которые являются оптимальными. Каждому из игроков невыгодно отклоняться от своей оптимальной стратегии, так как это может привести лишь к ухудшению его положения. Пара оптимальных стратегий игроков образуют решение игры, которое называется равновесием.
Если игра, заданная матрицей, не имеет седловой точки, то для нахождения ее решения используются смешанные стратегии. Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называется смешанной стратегией данного игрока => сумма компонент данного вектор =1, а сами эти коэффициенты не отрицательны. Обычно смешанную стратегию I игрока обозначают через U=(U1, …, Un). Ui≥0, i=1,m.
i=1Σm Ui=1
Стратегии 2 игрока:
Z=(Z1, …, Zn).
Zj≥0, j=1,n.
j=1Σn Zj=1
Всякая матричная игра с нулевой суммой имеет решение в смешанных стратегиях. Если U* - оптимальная стратегия I игрока, а Z* - оптимальная стратегия 2 игрока, то число V= j=1Σn i=1Σm aij Ui* Zj* является ценой игры, а совокупность {U*, Z*, V*} –решением игры. Для того, чтобы число V было ценой игры, а U* и Z* - оптимальными стратегиями, необходимо и достаточно, чтобы выполнялись следующие неравенства:
| i=1Σm aij Ui* ≥ V j=1,n | j=1Σn aij Zj*≤V i=1,m |
Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры V вне зависимости от того, с какими частотами будет применять 2 игрок стратегии, вошедшие в оптимальные (в т.ч и чистые стратегии).
45. Графическо представление игры при n=2
Предположим, что игрок 1 имеет m чистых стратегий, а игрок 2 - две чистых стратегии.
Тогда платежная матрица игры выглядит так:
| ( | a11 | a12 | ) | |
| A= | a21 | a22 | ||
| … | … | |||
| am1 | am2 |
Множество смешанных стратегий игроков имеет следующий вид:
- для игрока 1 – U={u=(u1,….,um), u1 + … + um=1; xi>=0, i=1,m};
- для игрока 2 – Z={z=(1-t, t), 0=<t=<1}
Обозначим R1(t), i=1,m – проигрыш игрока 2 в ситуации, когда он выбрал смешанную стратегию y=(1-t, t), а игрок 1 – свою чистую стратегию. Тогда ясно, что R1(t)=ai1(1-t)+ai2t.
Обозначим R(t)=max Ri(t), 1=<i=<m. Для игрока 2 оптимальной будет стратегия у*=(1-t*, t*), которой соответствует значение t*, дающее минимум функции R(t) на отрезке [0;1]. Функция R(t) будет выпуклой кусочно-линейной функцией на отрезке [0;1]. Она является верхней огибающей семейства прямых {Ri(t), i=1,m}, а ее минимум равен цене игры.
Тогда согласно Теореме 1 все стратегии игрока 1, для которых R1(t*)=v*, могут быть отброшены. Как правило, активными будут лишь две стратегии этого игрока, что также позволяет свести решение игры m x 2 к случаю 2 х 2.
Теорема 1. Если выигрыш игрока 1 в ситуации, образованной его чистой стратегией и оптимальной стратегией другого игрока, меньше цены игры, то такая чистая стратегия не может быть активной, и в любой оптимальной чистой стратегии вероятность ее использования равна нулю.
Проиллюстрируем использование графического метода в этом случае на примере.
Нужно найти решение игры, задаваемое матрицей.
| ( | -2 | ) | ||
| A= | -1 | |||
| -1 |
Проверим, есть ли у этой игры решение в чистых стратегиях. Для этого найдем max(i)min(j) aij = max {-2, -1, 1}=-1 и min(j)max(i) aij = min {2, 3}=2. Так как они не равны друг другу, то решения в чистых стратегиях нет.
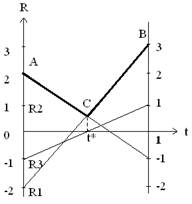
На оси Ot плоскости tOR отложим единичный отрезок [0, 1]. Каждой его точке t соответствует смешанная стратегия y=(1-t, t) игрока 2. Затем через точки 0 и 1 проведем линии, перпендикулярные оси Ot. На первом перпендикуляре, совпадающим с осью OR, отложим значения элементов первого столбца матрицы А – проигрыши игрока 2 при выборе им чистой стратегии В1. На втором перпендикуляре отложим значения элементов второго столбца – проигрыши игрока 2 при выборе им чистой стратегии В2. Затем соединим отрезками прямых точки на перпендикулярах, соответствующие чистым стратегиям игрока 1 – строкам матрицы А. Эти отрезки прямых являются графиками функций R1(t), задаваемых следующими уравнениями:
R1|(t) = -2(1-t) + 3t = -2+5t
R2|(t) = 2(1-t) - t = 2-3t
R3|(t) = -(1-t) + t = -1+2t
Затем построим из верхнюю огибающую – график функции R(t). На рисунке (1) она представлена ломаной АВС. Ее точка В, имеющая минимальную ординату, является графическим решением игры.
Из рисунка (1) видно, что точка В лежит на пересечении отрезков прямых R1 и R2. Значит, активными стратегиями игрока 1 являются стратегии А1 и А2. Стратегия А3 в его оптимальной стратегии не используется, т.е. х3*=0. Поэтому третью строку матрицы А можно вычеркнуть и рассмотреть игру с платежной матрицей
| ( | -2 | ) | x1 | ||
| А’= | -1 | x2 | |||
| y1 | y2 |
 Для определения цены этой игры и оптимальной смешанной стратегии игрока 1 следует решить систему уравнений:
Для определения цены этой игры и оптимальной смешанной стратегии игрока 1 следует решить систему уравнений:
-2х1+2х2=v
3x1-x2=v
x1+x2=1.
x1*=3/8, x2*=5/8, v*=1/2.
 Для нахождения коэффициентов активных стратегий игрока 2 нужно решить систему уравнений:
Для нахождения коэффициентов активных стратегий игрока 2 нужно решить систему уравнений:
-2y1+3y2=1/2
y1+y2=1
Ее решение y1*=1/2, y2*=1/2. Итак, исходная игра имеет решение: х*=(3/8; 5/8; 0), y*=(1/2; ½), v*=1/2.
Поиск по сайту: