 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Элементы теории
Симплекс-метод является методом линейного программирования, реализующий рациональный перебор базисных допустимых решений в виде конечного итеративного процесса, необходимо улучшающего значение целевой функции на каждом шаге. Метод был разработан американским математиком Джорджем Данцигом (George Dantzig) в 1947 году.
Последовательность вычислений симплекс-методом можно разделить на две основные фазы:
1. нахождение исходной вершины множества допустимых решений,
2. последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.
При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно является допустимым решением, хотя и, скорее всего, далеко не самым оптимальным). В таких задачах первую фазу симплекс-метода можно вообще не проводить. Симплекс-метод, соответственно, делится на однофазный и двухфазный.
Применение симплекс-метода для задачи линейного программирования предполагает предварительное приведение ее формальной постановки к канонической форме с n неотрицательными переменными: (X1,..., X n), где требуется минимизация линейной целевой функции при m линейных ограничениях типа равенств. Среди переменных задачи выбирается начальный базис из m базисных переменных, для определенности (X1,..., X m), которые должны иметь неотрицательные значения и остальные (n-m) свободные переменные равные 0. Целевая функция и ограничения равенства преобразуются к диагональной форме относительно базисных переменных. Каждая базисная переменная входит только в одно уравнение с коэффициентом 1:
X0 + A0,m+1*Xm+1 +... + A0,n*Xn = A0,0
X1 + A1,m+1*Xm+1 +... + A1,n*Xn = A1,0
………………….
Xi + Ai,m+1*Xm+1 +... + Ai,n*Xn = Ai,0
………………….
Xm + Am,m+1*Xm+1 +... + Am,n*Xn = Am,0
Данная формальная модель задачи линейного программирования обычно задается в форме, так называемой симплекс-таблицы, удобной для выполнения операций симплекс-метода:
Симплекс-таблица
| Аi,0 | X1 | X2 | ... | Xm | Xm+1 | ... | Xn | |
| X0 | A0,0 | ... | A0,m+1 | ... | A0,n | |||
| X1 | A1,0 | ... | A1,m+1 | ... | A1,n | |||
| X2 | A2,0 | ... | A2,m+1 | ... | A2,n | |||
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| Xm | Am,0 | ... | Am,m+1 | ... | Am,n |
Верхняя строка симплекс-таблицы представляет целевую функцию задачи. Каждая строка симплекс-таблицы, кроме первой, соответствует определенному ограничению-равенству задачи. Свободные члены ограничений составляют крайний левый столбец таблицы. В левом столбце таблицы записаны текущие базисные переменные (X1,..., X m). В верхней строке таблицы приведен набор всех переменных задачи, где X m +1,..., X n - свободные переменные задачи.
Преобразования таблицы надо производить до тех пор, пока не будет получена симплекс-таблица, которая одновременно является прямо и двойственно допустимой. Данный метод получил широкое распространение и большую популярность по сравнению с другими подходами, так как крайне редко на практике встречаются трудные для симплекс-метода задачи.
В рассматриваемом примере:
1) Приведение задачи к стандартному виду.
Вводя вспомогательные (балансовые) переменные x3 и x4 в левые части неравенств (А) и (Б), запишем ограничения в виде уравнений:
x1 + 2x2 + x3 = 3 (А)
3x1 + x2 + x4 = 3 (Б)
Целевая функция Z = 2x1 + x2 при приведении задачи к стандартному виду записывается так:
Z - 2x1 - x2 = 0 (С)
2) Составление первой симплекс-таблицы.
Симплекс-таблица составляется из коэффициентов при x1, x2, x3, x4 и чисел, стоящих в правых частях уравнений-ограничений задачи: в первой строке записываются коэффициенты и правая часть целевой функции (С). Далее по строкам записываются во второй – элементы уравнения (А), во второй - (Б). Таким образом, симплекс-таблица содержит строку коэффициентов целевой функции и две строки коэффициентов (по числу ограничений задачи). Число столбцов в симплекс-таблице равно числу переменных задачи плюс один столбец левых частей (Аi,0):
| Аi,0 | X1 | X2 | X3 | X4 |
| -2 | -1 | |||
Переменные, для которых столбцы коэффициентов состоят из одной единицы и нулей, называются базисными (в приведенном примере x3 и x4 - базисные переменные). Число базисных переменных равно числу ограничений задачи и не меняется при симплекс-преобразовании. Остальные переменные называются свободными (x1 и x2).
Симплекс-таблица определяет частное решение системы уравнений-ограничений:
 x1 +2x2 + x3 = 3 (А)
x1 +2x2 + x3 = 3 (А)
3x1 +x2 + x4 = 3 (Б),
при которых свободные переменные равны нулю (x1= 0, x2= 0), а базисные переменные равны правым частям соответствующих строк (x3= 3, x4= 3).
Значение целевой функции Z всегда равно числу, стоящему в левом верхнем углу таблицы (Z = 2·0+1·0=0). Первая симплекс-таблица соответствует начальному решению задачи ЛП (х1= 0, х2= 0, x3= 3, x4= 3, Z = 0). Это решение соответствует вершине А многоугольника допустимых решений ABCD (см. рис. 3).
Симплекс-метод состоит в последовательном перемещении по вершинам многоугольника допустимых решений. Каждой вершине соответствует своя симплекс-таблица, которая получается из предыдущей при помощи симплекс-преобразования.
В качестве разрешающего столбца берут столбец, у которого коэффициент в строке целевой функции является отрицательным и наибольшим по модулю (поскольку задача максимизации функции, а в задачах минимизации – наоборот). Если в данной симплекс-таблице строка целевой функции не содержат отрицательных коэффициентов, то решение задачи ЛП закончено и симплекс-таблица определяет решение задачи, при котором целевая функция Z принимает максимальное значение.
Разрешающая строка определяется по отношениям коэффициентов столбца Аi,0 к соответствующим коэффициентам разрешающего столбца. Разрешающей будет строка, для которой это отношение минимально. При, этом для нулевых и отрицательных коэффициентов разрешающего столбца отношения не вычисляются.
На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент.
Для первой симплекс-таблицы разрешающим столбцом является второй столбец (свободная переменная x1 будет преобразована в базисную). Среди отношений коэффициентов столбца Аi,0 к коэффициентам разрешающего столбца: 3/1 и 3/3 минимальным будет отношение 3/3: разрешающей строкой будет третья строка (базисная переменная x4 будет преобразована в свободную).
| Аi,0 | X1 | X2 | X3 | X4 |
| -2 | -1 | |||
 3 3
| 3 |

Задача симплекс преобразования состоит в том, чтобы на месте разрешающего элемента получить единицу, а все остальные элементы разрешающего столбца сделать нулевыми.
При этом допускается выполнение только двух операций со строками симплекс таблицы:
а) разрешающую строку можно делить (умножать) на любое число;
б) из любой строки можно вычитать элементы разрешающей строки или к любой строке можно прибавлять элементы разрешающей строки.
Выполним преобразование первой симплекс-таблицы.
1) Делим элементы разрешающей строки на 3:
| Аi,0 | X1 | X2 | X3 | X4 |
| -2 | -1 | |||
| 1/3 | 1/3 |
2) Из элементов первый строки вычитаем элементы второй (разрешающей) строки:
| Аi,0 | X1 | X2 | X3 | X4 |
| -2 | -1 | |||
| 5/3 1/3 | -1/3 1/3 |
3. К элементам третьей строки прибавляем элементы разрешающей строки, предварительно умножив их на два:
| Аi,0 | X1 | X2 | X3 | X4 |
| -1/3 | 2/3 | |||
| 5/3 1/3 | -1/3 1/3 |
Преобразование закончено. Полученной симплекс-таблице соответствует следующее решение:
базисные переменные: x1= 1, x3= 2,
свободные переменные: x2= 0, x4= 0.
Точка с координатами x1= 1, x2= 0 – это вершина D (см. рис.3). Значение целевой функции Z(D) = 2.
Так как в строке коэффициентов целевой функции есть отрицательный коэффициент (-1/3 во третьем столбце), то преобразование продолжается. Третий столбец является разрешающим (свободная переменная x2 переводится в базисную), минимальным среди отношений:  и
и  является первое число, следовательно, разрешающей строкой является вторая строка (базисная переменная x3 переводится в свободную).
является первое число, следовательно, разрешающей строкой является вторая строка (базисная переменная x3 переводится в свободную).
| Аi,0 | X1 | X2 | X3 | X4 |
| -1/3 | 2/3 | |||
 2 2
| 5/3 1/3 | -1/3 1/3 |

Выполнив симплекс-преобразование, получим:
| Аi,0 | X1 | X2 | X3 | X4 |
| 12/5 | 1/5 | 3/5 | ||
| 6/5 3/5 | 3/5 | -1/5 1/3 |
Так как в строке коэффициентов целевой функции нет отрицательных, решение задачи закончено.
Оптимальное решение:
базисные переменные: x1*=3/5= 0,6; x2*=6/5=1,2;
свободные переменные: x3*= 0; x4*= 0.
Точка с координатами x1*= 0,6 и x2*= 1,2 это вершина С (см. рис. 1.3)
Максимальное значение дохода (целевая функция):
Z*(С) = 12/5 = 2,4.
Задание 3. Решение задачи распределения ресурсов в MS EXCEL.
В рассматриваемом примере:
1) Ввод данных примера 1 в таблицу MS EXCEL (рис. 1.4).

Рис. 1.4.
На рис. 1.4 «консервы натуральные 1» обозначает консервы натуральные, «консервы бланшированные 2» – консервы бланшированные.
Для переменных задачи x1 и x2 отведены ячейки B3 и C3. Эти ячейки называются рабочими или изменяемыми ячейками. В изменяемые ячейки ничего не заносится и в результате решения задачи в этих ячейках будет оптимальные значения переменных.
В ячейку D4 вводится формула для вычисления целевой функции задачи (дохода) Z = 2x1 + x2. Чтобы сделать это, надо выполнить следующие действия:
курсор в D4;
курсор на кнопку f x (мастер функций);
В появившемся окне выбрать «Математические» и «СУММПРОИЗВ» (рис. 1.5).
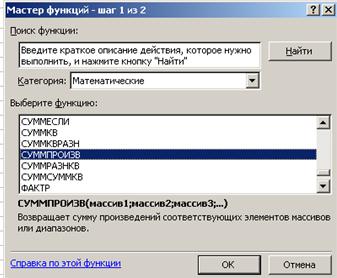
Рис. 1.5.
В окне мастера функций нажать Далее>, в появившемся окне (рис. 1.6) в поле «массив 1» ввести (протаскивая курсор мыши по ячейкам) адреса изменяемых ячеек B3:C3. В поле «массив 2» вводятся адреса ячеек содержащих цены на консервы B4:C4, после нажать Готово.

Рис. 1.6.
В ячейку D7 вводится формула для вычисления израсходованного количества продукта А: x1+2x2, а в ячейку D8 вводится формула для израсходованного количества продукта B: 3x1+x2. Обе формулы вводятся аналогично целевой функции (рис. 1.7 и 1.8).

Рис. 1.7.

Рис. 1.8.
Проверить результаты ввода можно следующим образом: при установке курсора в ячейку D4 в строке ввода должно появиться: «=СУММПРОИЗВ(B3:C3; B4:C4)»; в ячейки D7: «=СУММПРОИЗВ(B3:C3; B7:C7)»; в ячейки D8: «=СУММПРОИЗВ(B3:C3; B8:C8)».
Окончательно после ввода формул и данных экран имеет вид (рис. 1.9):

Рис. 1.9.
2) Работа в окне «Поиск решения»
В меню «Сервис» выбираем процедуру «Поиск решения»
В появившемся окне (рис. 1.10) нужно установить адрес целевой ячейки D4, значение целевой ячейки: максимальное, адреса изменяемых ячеек B3:C3.

Рис. 1.10.
Чтобы ввести ограничения задачи, нажать кнопку «Добавить». В появившемся диалоговом (рис. 1.11) окне слева ввести адрес D7 (израсходованное количество продукта А), затем выбрать знак <= и в правой части количество продукта А на складе, равное 3 (или адрес ячейки E7).

Рис. 1.11.
После ввода нажать кнопку «Добавить» и аналогично ввести второе ограничение: D8 <= 3. Снова нажать кнопку «Добавить» и ввести ограничение: B3:C3 >= 0 (соответствующее ограничению x1, x2 >= 0). После ввода последнего ограничения нажать ОК. После ввода ограничений окно «Поиска решений имеет» будет иметь вид (рис. 1.12):

Рис. 1.12.
3) Настройка параметров решения задачи.
В окне «Поиск решения» нажать «Параметры» в появившемся окне (рис. 1.13) установить флажок в пункте «Линейная модель». В этом случае при решении задачи будет использоваться симплекс-метод. Остальные значения можно оставить без изменения. После нажать кнопку ОК.

Рис. 1.13.
Для решения задачи в окне «Поиск решения» нажать кнопку «Выполнить». Если решение найдено появляется окно (рис. 1.14):

Рис. 1.14
Для просмотра результатов выбираем тип отчета: «Результаты» и нажимаем кнопку ОК. В появившихся трех таблицах (рис. 1.15) приводятся результаты поиска.

Рис. 1.15.
Из этих таблиц видно, что в оптимальном решении:
производство консервов натуральных = B3 = 0.6;
производство консервов бланшированных = С3 = 1.2;
при этом доход = D4 = 2.4;
расход сырья A = D7 = 3;
расход сырья B = D8 = 3.
Таким образом, оба ресурса дефицитные (соответствующие ограничения называются связанными).
«Отчет по результатам» состоит из трех таблиц (рис. 1.15):
в таблице 1 приводятся сведения о целевой функции;
в таблице 2 приводятся значения переменных задачи;
в таблице 3 показаны результаты поиска задачи.
Первоначальная таблица MS EXCEL заполняется результатами, полученными при решении (на рис. 1.16 появившиеся значения в темных ячейках).

Рис. 1.16.
Контрольные вопросы
1. Какая задача оптимизации называется задачей линейного программирования?
2. На чем основан графический метод решения задач оптимизации?
3. Какая графическая интерпретация определяет на координатной плоскости каждое из неравенств задачи линейного программирования и систему неравенств в целом?
4. Что называется ОДР? Как графически представляется ОДР на координатной плоскости и какими свойствами обладает?
5. Как графически может быть представлена ОДР?
6. В каком случае ОДР является пустым множеством?
7. Как получить линии уровня? Почему для решения задачи графическим методом будет достаточно построить одну из линий уровня?
8. Как располагается вектор с координатами из коэффициентов ЦФ относительно линий уровня и как его направление влияет на решение задачи оптимизации?
9. В чем суть графического метода решения задачи оптимизации?
10. Какие ситуации возможны при поиске оптимального решения задач линейного программирования?
11. Что реализует симплекс-метод решения задач линейного программирования?
12. На какие две основные фазы можно разделить последовательность вычислений симплекс-методом?
13. Что предполагает применение симплекс-метода для задачи линейного программирования?
14. В чем состоит задача симплекс преобразования?
15. Какие преобразования происходят с целевой функцией и уравнениями-ограничениями?
16. Какие значения вводятся в строки и столбцы при формализации симплекс-таблицы? Чему соответствует каждая строка симплекс-таблицы?
17. Какие переменные в симплекс-таблице являются базисными, а какие свободными? Чему равно число базисных переменных?
18. Как найти разрешающий столбец и разрешающую строку при симплекс преобразовании?
19. Какие операции допускаются при симплекс преобразовании?
20. При решении задачи о распределении ресурсов в компьютерной программе MS EXCEL какие ячейки будут рабочими или изменяемыми и что в них отражено?
21. С помощью какой процедуры решается задача распределения ресурсов в компьютерной программе MS EXCEL?
22. Какие действия необходимо предпринять, чтобы для решения задачи в компьютерной программе MS EXCEL был использован симплекс-метод?
23. Что включает в себя «Отчет по результатам» при решении задачи о распределении ресурсов в компьютерной программе MS EXCEL?
Поиск по сайту: