АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача определения максимального потока в сети

Читайте также:
  1. I Определения
  2. I. 3.1. Двойственная задача линейного программирования
  3. I. Дайте определения следующих правовых категорий.
  4. I. Открытые способы определения поставщика.
  5. I. Функции эндоплазматической сети.
  6. II. Исследование пульса, его характеристика. Места определения пульса.
  7. II.2. Задача о назначениях
  8. II.4. МЕТОД ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
  9. III. Используемые определения и обозначения
  10. VI. Общая задача чистого разума
  11. Алгоритм определения валютно-правового статуса ценных бумаг
  12. Алгоритм определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы с положительными элементами.

Рассмотрим в качестве функциональной модели совокупности серверов параллельную сеть массового обслуживания со случайным ветвлением заявок (рис. 2.2.1.). Каждый сервер представим одноканальной системой массового обслуживания M/M/1. Предполагается, что общий входной поток в сеть λ является переменной величиной, причём при изменении λ отношение λi / λ сохраняется постоянным (распределение заявок по серверам рi i=1,2,… N с изменением нагрузки не меняется). Производительность каждой системы μi задана. С ростом нагрузки λ растёт средняя задержка любой заявки в сети. Под пропускной способностью сети понимается такая максимальная нагрузка λ, при которой средняя задержка любой заявки в сети будет равна допустимой величине Т. Дальнейший рост нагрузки приводит к увеличению задержки на величину больше Т.

Постановка задачи определениямаксимального потока в сети будет иметь вид:

Дано:

· N – изолированных серверов и их модели в виде систем М/М/1

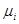· - производительность каждого сервера i=1,2,…N,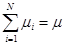

· Pi -распределение потока λ по серверам, Pi = λi/ λ – константы, i = 1,……N

Найти: такую нагрузку на сеть λ (и соответственно на каждый сервер λi), при которой суммарный поток через сеть будет максимальным:

λ = 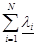= 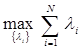, (5.1)

Ограничения:

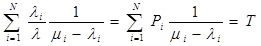(5.2.)

, i = 1,……N

Решение:

Рассмотрим критериальную функцию (5.1). Критериальная функция является аддитивной функцией величин λi, каждая из которых есть линейна (выпукла). Тогда критериальная функция (5.1) также будет выпукла.Докажем это. Найдём частные производные функций (5.1) и (5.2.).

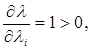
i = 1,……N (5.3.)

i = 1,……N (5.4.)

Из (5.3) видно, что вторая производная критериальной функции равна нулю, следовательно функция выпукла как сумма линейных слагаемых. Ограничение (5.4) также является выпуклым (вторая производная функции больше нуля). Тогда ло­кальный минимум задачи будет глобальным и можно применить метод множителей Лагранжа. Образуем функцию Лагранжа:

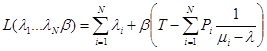
Имеем функцию N+1 переменной без ограничений. Дифференцируя её по λi,β, i = 1, 2,…N и приравнивая результат к нулю получаем систему N+1уравнений с N+1 неизвестными:

 

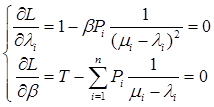i = 1, 2,…N (5.5)

Из (5.5) получим:

i = 1, 2,…N (5.6)

Подставив λi из (5.6) в (5.5) получим

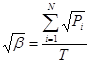
Или окончательно из (5.6) находим:

i = 1, 2,…N (5.7.)

Складывая правые и левые части системы уравнений (5.7) получаем решение задачи

, λ i=λ Pi i = 1, 2,…N (5.8.)


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)