Задача определения оптимальной производительности серверов информационно - вычислительной сети

Рассмотрим схему технических средств КИС, приведенную на рис. 2.1.1. Одной из главных задач является выбор оборудования для центрально вычислительного комплекса (ЦВК). Центральный вычислительный комплекс обеспечивает хранение и обработку корпоративных данных. Доступ конечных пользователей к прикладным процессам обработки, функционирующим на серверах ЦВК, а через них - к корпоративным данным, решается с помощью сети доступа. При объединении ПЭВМ и серверов с помощью средств передачи данных клиенты получили возможность работать со многими приложениями на специализированных серверах. Данные распределяются между серверами в зависимости от потребностей прикладных задач,

Рис. 2.1.1. Схема ЦВК регионального оператора связи

Состав, типы и мощности серверов определяются индивидуально для каждого регионального оператора связи, интенсивности запросов и перечня оказываемых услуг, а также с учётом перспектив развития.

Рассмотрим простейшую структурную модель ЦВК в виде параллельно функционирующих несвязанных серверов (рис. 2.1.2.)

Рис. 2.1.2. Структурная модель ЦВК.

Поступающая в ЦВК нагрузка распределяется диспетчером между серверами в соответствии с вероятностями P₁…. Р_N. Оптимальное обслуживание входящей нагрузки связано с согласованием производительности каждого сервера с заданной диспетчером для этого сервера нагрузкой при условии, что средняя задержка любого сообщения в сети будет минимальной.

В качестве функциональной модели ЦВК примем открытую параллельную сеть массового обслуживания со случайным ветвлением заявок. Каждый сервер будем моделировать одноканальной системой массового обслуживания M/M/1. Предполагается что известен входной поток заявок в сеть и вероятности передач (распределение) заявок по системам (рис. 2.1.3).

Рис. 2.1.3 Функциональная модель ЦВК сети.

Постановка задачи оптимизации производительности серверов ЦВК.

Дано:

N – изолированных серверов и их модели в виде систем М/М/1

- общий входной поток заявок в сеть

- общая производительность ЦВК

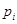- вероятности распределения заявок по серверам, i = 1, 2…N, так что

Найти: такие производительности серверов ЦВК μ ₁….. μ _N, при которых средняя задержка любого задания в сети будет минимальной:

(2.1)

Ограничения:

(2.2)

i=1,2,…N

Решение:

Рассмотрим критериальную функцию (2.1). Критериальная функция является аддитивной функцией величин Tq_i, каждая из которых есть выпуклая функция μ_i. Тогда критериальная функция (2.1) также будет выпукла.Докажем это. Найдём частные производные

(2.3)

Видно, что вторая производная критериальной функции больше нуля, следовательно функция выпукла как сумма выпуклых слагаемых. Ограничение (2.2) также является выпуклым как сумма линейных слагаемых. Тогда локальный минимум задачи будет глобальным и можно применить метод множителей Лагранжа для поиска минимума.Образуем функцию Лагранжа:

Имеем функцию N+1 переменной без ограничений. Дифференцируя её по µ_i,β, i = 1, 2,…N и приравнивая результат к нулю получаем систему N+1уравнений с N+1 неизвестными:

Из (2.4) получим (2.6)

i=1,2,….N

Суммируя (2.6) и используя (2.5) получим:

(2.7)

Из (2.7) найдем , откуда неизвестный множитель Лагранжа будет равен

(2.8)

Подставляя выражение (2.8) в (2.7) получим решение задачи:

i=1,2,…N (2.9)

Подставляя в критериальную функцию (2.1), найдем минимальное значение средней задержки T⁰_q(μ ₁,… μ _N/λ₁,…λ_N)

= (2.10)

Следствия.

1. достигает минимума по переменным λ_i при равномерном распределении потока задач по серверам, когда :

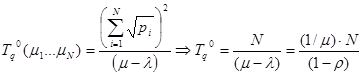
2.Оценки снизу и сверху для минимального значения средней задержки имеют вид:

Поиск по сайту: