АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача определения оптимального распределения нагрузки по серверам в равномернозагруженных информационно - вычислительных сетях

Читайте также:
  1. FSBFRUL (Ф. Правило распределения ассигнований по КЭКР.Заголовки)
  2. I Определения
  3. I. 3.1. Двойственная задача линейного программирования
  4. I. Дайте определения следующих правовых категорий.
  5. I. Открытые способы определения поставщика.
  6. I. Случайные величины с дискретным законом распределения (т.е. у случайных величин конечное или счетное число значений)
  7. II. Исследование пульса, его характеристика. Места определения пульса.
  8. II.2. Задача о назначениях
  9. II.4. МЕТОД ВЕТВЕЙ И ГРАНИЦ В ЗАДАЧАХ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ
  10. III. Используемые определения и обозначения
  11. III. Определение оптимального уровня денежных средств.
  12. III. Создание и обработка комплексного информационного объекта в виде презентации с использованием шаблонов.

В качестве функциональной модели совокупности серверов рассмотрим параллельную сеть массового обслуживания со случайным ветвлением заявок. Каждый сервер представим одноканальной системой массового обслуживания M/M/1. Предполагается, что известен общий входной поток в сеть λ и производительность каждой системы μi (рис. 2.2.1.) Оптимальное обслуживание входящей нагрузки связано с таким согласованием нагрузки каждого сервера с его производительностью при котором загрузки всех систем 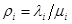i=1,2,…N будут равны.

Постановка задачи оптимального распределения нагрузки между серверами ЦВК в равномерно загруженных информационно - вычислительных сетях будет иметь вид:

Дано:

§ N – изолированных серверов и их модели в виде систем М/М/1

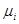§ - производительность каждого сервера i=1,2,…N

§ - общий входной поток заявок в сеть

Найти: такую нагрузку на каждый сервер i=1,2,…N при которой максимально загруженная система сети будет иметь минимальную загрузку (поток, который минимизирует загрузку сервера в наиболее загруженном месте сети)

 

min (max ) = min (max )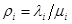

 

Ограничения:

i=1,2,…N,

Решение:

Для решения задачи постановку задачи можно переписать в эквивалентной формулировке, вводя новую переменную β0 и новые ограничения.

Найти: такие значения переменных β 0, λ i i=1,2,…N, которые минимизируют линейную аддитивную целевую функцию

β 0=min (4.1)

где = 1, i=1,2,… N

Ограничения:


..................

Ограничения можно переписать в виде:

 

…………

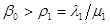
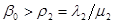
(4.2.)

 

Исходную минимаксную задачу свели к задаче линейного программирования (4.1), (4.2), которая решается графически при двух переменных и численно симплекс- методом в общем случае.

 

 


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)