Задача определения оптимального распределения нагрузки по серверам информационно - вычислительной сети

Рассмотрим задачу оптимального распределения нагрузки между серверами ЦВК при условии что производительность каждого сервера задана. Схема технических средств информационно-вычислительной системы приведена на рис. 2.1.1, а структурная модель ЦВК на рис. 2.1.2. Оптимальное обслуживание входящей нагрузки связано с таким согласованием нагрузки для каждого сервера с заданной производительностью сервера при которой средняя задержка любого сообщения в сети будет минимальной.

В качестве функциональной модели совокупности серверов рассмотрим параллельную сеть массового обслуживания со случайным ветвлением заявок. Каждый сервер представим одноканальной системой массового обслуживания M/M/1. Предполагается, что известен общий входной поток в сеть λ и производительность каждой системы μ_i (рис. 2.2.1.)

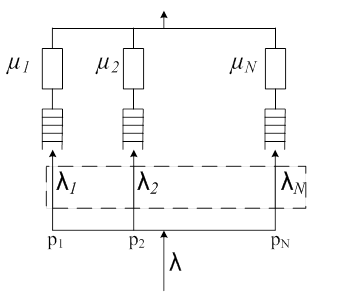
Рис. 2.2.1. Функциональная модель ЦВК сети.

Постановка задачи оптимального распределения нагрузки между серверами ЦВК будет иметь вид:

Дано:

N – изолированных серверов и их модели в виде систем М/М/1

- общий входной поток заявок в сеть

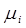- производительность каждого сервера i=1,2,…N, так что .

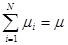Найти: такую нагрузку на каждый сервер λ _i, при которой средняя задержка любого задания в сети будет минимальной

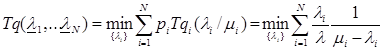(3.1)

Ограничения:

(3.2)

i=1,2,…N,

Решение:

Рассмотрим критериальную функцию (3.1). Критериальная функция является аддитивной функцией величин Tq_i, каждая из которых есть выпуклая функция по λ_i. Тогда критериальная функция (2.1) также будет выпукла.Докажем это. Найдём частные производные

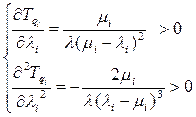i=1,2,…N (3.3)

Из (3.3) видно, что вторая производная критериальной функции больше нуля, следовательно функция выпукла. Ограничение (3.2) также является выпуклым как сумма линейных слагаемых. Тогда ло­кальный минимум задачи будет глобальным и можно применить метод множителей Лагранжа. Образуем функцию Лагранжа:

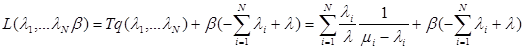
Имеем функцию N+1 переменной без ограничений. Дифференцируя её по λ_i,β, i = 1, 2,…N и приравнивая результат к нулю получаем систему N+1уравнений с N+1 неизвестными:

Из (3.4) найдём решение 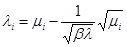i=1,2,…N (3.6)

Суммируя (3.6) и используя (3.5) получим выражение для определения неизвестного множителя Лагранжа:

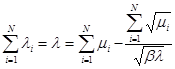(3.7)

Из (3.7) найдем , откуда получим неизвестный множитель Лагранжа

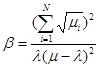(3.8)

Подставляя (3.8) в (3.6) окончательно получим решение задачи:

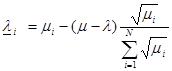(3.9)

Подставим 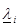в критериальную функцию (3.1.) найдем минимальное значение средней задержки T⁰_q(λ₁,… λ_N/μ₁,…μ_N)

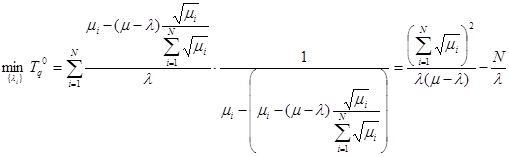(3.10)

Или (3.10) можно переписать в другом виде:

Следствия:

1. В случае равномерного распределения ресурсов 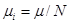минимальное значение задержки совпадает с выражением для минимального значения задержки при оптимальном распределении нагрузки

2. Распределение нагрузки лучше (меньше задержка), чем распределение ресурсов

Поиск по сайту: