Регрессионный анализ. Как и прежде, будем описывать функционирование исследуемого реального объекта (фирмы, компании, процесса производства или дистрибуции продукции и т

Как и прежде, будем описывать функционирование исследуемого реального объекта (фирмы, компании, процесса производства или дистрибуции продукции и т. п.) набором переменных и (их содержательный смысл описан в п. 2). Введем ряд определений и понятий, используемых в регрессионном анализе.

Результирующие (зависимые, эндогенные) переменные. Переменная 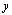, характеризующая результат или эффективность функционирования анализируемой системы, называется результирующей (зависимой, эндогенной). Ее значения формируются в процессе и внутри функционирования этой системы под воздействием ряда других переменных и факторов, часть из которых поддается регистрации и, в определенной степени, управлению и планированию (эту часть принято называть объясняющими переменными, см. ниже). В регрессионном анализе результирующая переменная выступает в роли функции, значения которой определяются (правда, с некоторой случайной погрешностью) значениями упомянутых выше объясняющих переменных, выступающих в роли аргументов. Поэтому по природе своей результирующая переменная 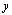всегда стохастична (случайна). В общем случае обычно анализируется поведение сразу нескольких результирующих переменных .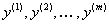

Объясняющие (предикторные, экзогенные) переменные . Переменные (или признаки), поддающиеся регистрации, описывающие условия функционирования изучаемой реальной экономической системы и в существенной мере определяющие процесс формирования значений результирующих переменных, называются объясняющими. Как правило, часть из них поддается хотя бы частичному регулированию и управлению. Значения ряда объясняющих переменных могут задаваться как бы «извне» анализируемой системы. В этом случае их принято называть экзогенными. В регрессионном анализе они играют роль аргументов той функции, в качестве которой рассматривается анализируемый результирующий показатель 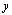. По своей природе объясняющие переменные могут быть как случайными, так и неслучайными.

Регрессионные остатки – это латентные (т. е. скрытые, не поддающиеся непосредственному измерению) случайные компоненты, отражающие влияние соответственно на 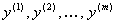не учтенных в составе факторов, а также случайные ошибки в измерении анализируемых результирующих переменных. Они, вообще говоря, тоже могут зависеть от , т. е. в общем случае .

Общая схема взаимодействия переменных в регрессионном анализе изображена на рисунке.

Рисунок. Общая схема взаимодействия переменных в регрессионном анализе.

Функция регрессии 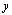по . Функция называется функцией регрессии по (или просто – регрессией 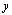по ), если она описывает изменение условного среднего значения результирующей переменной 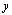(при условии, что значения объясняющих переменных зафиксированы на уровнях ) в зависимости от изменения значений объясняющих переменных. Соответственно математически это определение может быть записано в виде

,

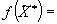
где символ означает операцию теоретического усреднения значений 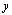(т. е. 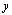– это математическое ожидание случайной величины 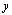, а , или просто – это условное математическое ожидание случайной величины 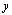, вычисленное при условии, что значения объясняющих переменных зафиксированы на уровне ).

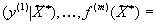
Если мы анализируем одновременно результирующих переменных , то следует рассмотреть соответственно функций регрессий или, что то же, одну векторнозначную функцию

. (11)

Тогда модель регрессии по может быть записана в виде

, (12)

причем, из определения следует, что всегда]

(12’)

(тождественный знак равенства в (12’) означает, что оно справедливо при любых значениях ; вектор-столбец из нулей в правой части имеет размерность ).

В рамках введенных понятий и обозначений задача регрессионного анализа в самом общем виде может быть сформулирована следующим образом:

по результатам измерений

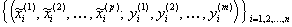
исследуемых переменных на объектах (системах, процессах) анализируемой совокупности построить такую (векторнозначную) функцию (11), которая позволила бы наилучшим (в определенном смысле) образом восстанавливать значения результирующих (прогнозируемых) переменных по заданным значениям объясняющих (экзогенных) переменных .

З а м е ч а н и е 1. Наиболее распространенными являются линейные модели регрессии, т. е. модели, в которых функции регрессии имеют линейный вид:

(12^’’)

З а м е ч а н и е 2. Существует по меньшей мере два варианта интерпретации введенных в п. 2 «поведенческих», «статусных» и «внешних» переменных, соответственно, и в рамках описанной модели регрессии (12)–(12’). В первом варианте все три типа переменных и относят к объясняющим переменным и строят регрессию по . В другом варианте переменные 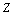и интерпретируют как условия проведения наблюдений и тогда отдельно для каждого фиксированного сочетания этих условий строят регрессионную модель вида (12) (в рамках линейной модели (12^’’) это будет означать, что сами коэффициенты регрессии зависят от 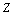и , т. е. 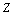определяются как функции от и ).

Поиск по сайту: