Механизмы формирования и статистический анализ экспертных оценок

Обычно выделяются следующие основные типы организации работы группы экспертов ([6]):

· коллегиальный: «метод комиссий» (в виде открытой дискуссии по обсуждаемой проблеме); «метод суда» (в виде противостояния «защиты» и «обвинения» по каждому из вариантов обсуждаемого решения проблемы); «мозговая атака» и т.п.;

· частично коллегиальный: сценарный анализ типа «что – если», метод «Делфи» – многотуровое обсуждение проблемы с тайным голосованием экспертов или заполнением специальных анонимных анкет в конце каждого тура и работой независимой аналитической группы в промежутках между турами и т.п.;

· индивидуально-автономный: каждый из участников экспертной группы формирует и высказывает свое мнение (независимо от позиций других участников) в виде ранжирования обсуждаемых вариантов решения (или объектов), их парных сравнений или отнесения каждого из них к одной из заранее описанных градаций (см. формы представления исходных статистических данных в виде таблиц частот или таблиц сопряженности в п. 1). Иногда эксперты должны оценивать вероятность наступления того или иного события.

При любом из упомянутых выше типов организации работы экспертов приходится проводить статистический анализ экспертных мнений. К основным задачам статистического анализа экспертных оценок относятся:

(i) Исследование структуры совокупности экспертных мнений. Эта задача решается средствами многомерного статистического анализа – методами ранговой корреляции, кластер-анализа, многомерного шкалирования и т.п. (см. [1], гл. 12, 13]. Так, если ответы экспертов и даны в виде упорядочений сравниваемых вариантов решения (или объектов) соответственно 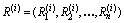и , то «расстояние» между мнениями -го и -го экспертов измеряют величиной , где – коэффициент ранговой корреляции Спирмена (см. [1], гл. 11]). Определив тот или иной способ вычисления «расстояния» между мнениями пары экспертов, мы можем решать затем задачу «кластеризации» экспертов, интерпретируя каждый из найденных таким образом кластер как группу экспертов-единомышленников.

(ii) Анализ взаимной согласованности мнений группы экспертов. Располагая мнениями целой группы экспертов, аналитик-статистик стремится оценить степень согласованности всех этих экспертных оценок, в том числе и статистически проверить гипотезу о полном отсутствии какой-либо их согласованности (и тогда, очевидно, следует либо уточнить постановку предложенной экспертам задачи, либо поменять состав экспертной группы). Эта задача также решается средствами многомерного статистического анализа. Выбор конкретного метода зависит от формы исходных статистических данных. Например, если мнения экспертов представлены ранжировками, то в качестве меры их согласованности можно рассматривать коэффициент конкордации Кендалла:

.

Близость величины к единице свидетельствует о высокой степени согласованности анализируемых мнений (при все мнения просто совпадают). Малые значения говорят об отсутствии какой бы то ни было согласованности в анализируемых мнениях (существует строгий статистический критерий проверки этой гипотезы (см. [1, гл. 11]).

(iii) Построение единого группового мнения и оценка относительной компетентности каждого эксперта. Поиск единого группового мнения сводится к решению соответствующей оптимизационной задачи. Так, например, при балльных экспертных оценках анализируемых вариантов решения (или объектов), т.е. при исходных статистических данных вида

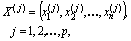
где – балльная оценка -го объекта (варианта решения), данная -м экспертом, единое групповое мнение является решением оптимизационной задачи вида

,

где с помощью обозначается решение оптимизационной задачи вида , т.е. .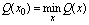

Если же исходные данные представлены в виде ранжировок (9), то единая групповая ранжировка определяется как решение оптимизационной задачи вида

где с помощью обозначена медиана ряда 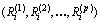, т.е. средняя по расположению величина , когда члены этого ряда расположены в порядке возрастания их величин.

Наконец, при задании мнения j -го эксперта в виде матрицы парных сравнений

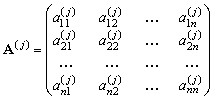
элементы матрицы парных сравнений группового мнения подбираются таким образом, чтобы

Основная идея различных подходов к оценке относительной компетентности каждого (j -го) эксперта, заключается в следующем: чем «дальше» мнение j -го эксперта отстоит от единого группового мнения, тем ниже оценивается уровень его относительной компетентности. Заметим, что если в результате исследования структуры совокупности экспертных мнений аналитик-статистик приходит к выводу о наличии нескольких подгрупп экспертов с однородностью мнений внутри каждой подгруппы и с существенным различием мнений в любой паре таких подгрупп, то задача единого группового мнения и оценка относительной компетентности эксперта решается отдельно для каждой из выявленных подгрупп.

[1] Случайные факторы, в свою очередь, могут быть двоякой природы: внезапными («разладочными»), приводящими к скачкообразным структурным изменениям в механизме формирования значений x(t) (что выражается, например, в радикальных скачкообразных изменениях основных структурных характеристик функций f _тр (t), j(t) и y(t) анализируемого временного ряда в случайный момент времени), и эволюционными остаточными, обусловливающими относительно небольшие случайные отклонения значений x(t) от тех, которые должны были бы получиться только под воздействием факторов (А), (Б) и (В). Однако в данном разделе будут рассмотрены схемы формирования временных рядов, включающие в себя действие только эволюционных остаточных случайных факторов.

Поиск по сайту: