 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Основні теоретичні положення. Дві накладені одна на другу поверхні дотикаються спочатку в трьох точках
Дві накладені одна на другу поверхні дотикаються спочатку в трьох точках. Під впливом навантаження поверхні зближаються і у дотик входить усе більша кількість окремих виступів. При цьому одна частина виступів, у яких напруження не перевищують межі текучості, деформуються пружно. Друга частина виступів деформується пластично. Таким чином, в міру наближення поверхонь зростає площа дотику. В теорії тертя сума фактичних малих площадок дотику тіл отримала назву площі фактичного контакту Аr.
Зміна фактичної площі контакту з навантаженням обумовлено розміщенням нерівностей по висоті, їх геометричним розташуванням, механічними властивостями, з яких найважливішими є модуль пружності, межа текучості, характеристики зміцнення матеріалу в результаті дії пластичних деформацій (наклеп).
Хвилястість поверхні визначає зони, в яких проходить контакт мікровиступів. Ці зони утворюють так звану контурну площу контакту Ас. Таким чином, контурна площа контакту Ас представляє собою площу, утворену об’ємним зминанням тіл, обумовленим хвилястістю. Величина контурної площі залежить від параметрів хвилястості та від навантаження.
Геометричним місцем всіх можливих фактичних і контурних площ контакту, площа, охоплена розмірами тіл, що дотикаються, її називають номінальною площею контакту – Аа.
Вказані площі схематично показані на рисунку 3.1.
Очевидно, що контурна і номінальна площі контакту є гіпотетичними поняттями, оскільки вони фіктивні. Контурна площа контакту вводиться як проміжна вітка для переходу від фактичної Аr до номінальної площі контакту Аа.
Поняттям “номінальна площа контакту” користуються в розрахунках, не зв`язаних з мікрогеометрією реальних тіл. У випадку плоских контактів – це площа, по якій дотикалися би тіла, маючи ідеально гладку поверхню.
|
 |
Існують багато методів визначення фактичної площі контакту. Від неї залежить область силової міжмолекулярної взаємодії двох шорстких тіл. По цій причині розрахунок площі фактичного контакту є однією із головних складових частин розрахунків тертя і зношування. В розрахунках зручно користуватися безрозмірними величинами, а саме
 ,
,  ,
,  . (3.1)
. (3.1)
 |
Зростання площі контакту поверхонь по мірі зближення під дією навантаження може бути визначено по так званій кривій опорної поверхні, яка будується на основі профілограми. Крива опорної поверхні (опорна крива) характеризує розподіл матеріалу по висоті шорсткого шару. Для її побудови профілограму розбивають на ряд горизонтальних рівнів, паралельних середній лінії. Потім сумуються частинки, які обмежують ширину виступів Dli на заданому рівні Р (рисунок 3.2).
Рисунок 3.2 - Схема побудови кривої опорної поверхні
Однак, якщо по осі ординат відкладати відстань від площини, що проходить через впадини поверхні до заданого рівня, то в цьому випадку форма кривої опорної поверхні буде залежати від максимальної висоти нерівностей і, в залежності від чистоти обробки, криві будуть мати різний характер. Тому крива опорної поверхні як правило будується в відносних величинах. В цьому випадку по осі ординат (рисунок 3.3) відкладається відносна величина
 , (3.2)
, (3.2)
де  , h – зближення.
, h – зближення.
По осі абсцис відкладають відношення суми перерізів виступів на даному рівні до довжини оброблюваної профілограми
 , (3.3)
, (3.3) 
де tp – відносна опорна довжина профілю.
При побудові кривої опорної поверхні у відносних величинах її форма не залежить від висоти нерівності. Форма кривих, побудованих таким чином, залежить тільки від конфігурації виступів і їх розподілу по висоті. Причому, початкова частина опорної кривої (в межах 0 < tp £ 0,5) з достатньою для інженерної практики точністю апроксимується степеневою залежністю
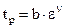 , (3.4)
, (3.4)
де: 
 - відношення фактичної площі контакту до контурної площі;
- відношення фактичної площі контакту до контурної площі;
|

b,v – параметри апроксимації початкової частини кривої опорної поверхні профілю.
Таким чином
 , (3.5)
, (3.5)
де tp – відносна опорна довжина на рівні середньої лінії;
Dlp - відстань між лінією виступів і середньою лінією в межах базової довжини.
Необхідно відмітити, що фактична площа контакту навіть при високих навантаженнях складає незначну долю від контурної, тому особливий інтерес при аналізі контактної взаємодії представляє саме частина кривої опорної поверхні, коли
 . (3.6)
. (3.6)
Таким чином, параметри степеневої апроксимації b i v початкової частини кривої опорної поверхні визначають характер розподілу нерівностей по висоті шорсткого шару.
Вказані параметри використовуються в розрахунках молекулярно-механічної теорії тертя і втомної теорії зношування.
Параметри b і v можуть бути визначені декількома методами. Однак графоаналітичний метод визначення при мінімальній трудоємкості дає достатньо достовірний опис. При цьому параметри апроксимації початкової частини опорної кривої визначаються в результаті рішення системи рівнянь, взятих для двох значень зближення e1 і e2

 (3.7)
(3.7)
Звідки
 , (3.8)
, (3.8)
 . (3.9)
. (3.9)
Найбільш доцільно визначати b i v для наступних трьох пар зближень
Група 1: Група 2:
а) e1 = 0,1 і e2 = 0,2; а) e1 = 0,05 і e2 = 0,1;
б) e1 = 0,1 і e2 = 0,3; б) e1 = 0,05 і e2 = 0,2;
в) e1 = 0,2 і e2 = 0,3. в) e1 = 0,1 і e2 = 0,2.
Вимірявши при кожному з цих зближень Dl і підставивши у формули (3.8) і (3.9), знаходимо для кожної пари зближень v1, v2, v3, i b1, b2, b3. Розрахункові значення b i v визначаються як середнє арифметичне із трьох
 , (3.10)
, (3.10)
 . (3.11)
. (3.11)
Група 1 зближень використовується при монотонному збільшенні площі із збільшенням зближення. Якщо ж при e = 0,3tpi, для визначення b і v слід використати групу 2 зближень.
У задачах визначення коефіцієнта тертя, інтенсивності зношування і контактної жорсткості спряження найбільш повну оцінку шорсткості поверхні дає безрозмірний критерій D, який отримав назву “комплексного критерію шорсткості”. Він (критерій Камбалова) об`єднує відношення найбільшої висоти нерівностей профілю Rmax до радіуса кривизни вершини нерівності r і параметри b та 1/v, які враховують розподіл нерівності по висоті
 . (3.12)
. (3.12)
Для більшості видів механічної обробки металів комплексний критерій шорсткості представляє собою табульовану величину і приводиться в довідниках разом з іншими параметрами шорсткості поверхні [6]. Для технологічно оброблених поверхонь комплекс D зв`язаний із значенням Ra залежністю
 , (3.13)
, (3.13)
де:  - безрозмірна величина, рівна відношенню
- безрозмірна величина, рівна відношенню  (мкм) до значення
(мкм) до значення 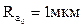 ;
;
с і  - константи виду обробки.
- константи виду обробки.
Поиск по сайту: