 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
И МОМЕНТОВ ЭЛЕКТРОМАГНИТА
При перемещении якоря электромагнита из положения 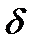 1 в положение
1 в положение 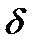 2,
2,
т. е. за путь 
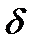 , им произведена работа
, им произведена работа  А. Следовательно, средняя сила притяжения Рср, действовавшая на этом отрезке,
А. Следовательно, средняя сила притяжения Рср, действовавшая на этом отрезке,
Рср =  А /
А / 
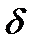 . (5-14)
. (5-14)
Переходя к пределу, получим формулы для вычисления сил и моментов притяжения якоря электромагнита:
Р = 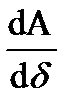 ;
;  , (5-15
, (5-15
где d 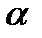 — угол поворота якоря, соответствующий изменению воздушного зазора на d
— угол поворота якоря, соответствующий изменению воздушного зазора на d 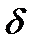 .
.
Подставив в уравнение (5-15) выражение (5-11) для dA, получим в общем случае
Р =  . (5-16)
. (5-16)
В электромагнитных системах, работающих при постоянной МДС, 1 == const и dI/d 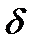 = 0, тогда
= 0, тогда
Р = 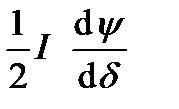 . (5-17)
. (5-17)
Согласно выражению (5-4)  = L I,, откуда
= L I,, откуда
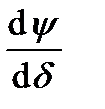 = I
= I  +
+ 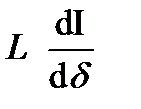 = I
= I 
так как при I = const, dI/d 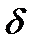 = 0, то
= 0, то
Р =  . (5-18)
. (5-18)
Учитывая, что L= 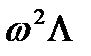 , где
, где 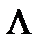 — проводимость воздушного зазора,
— проводимость воздушного зазора,  — число витков катушки, получим
— число витков катушки, получим
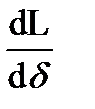 =
= 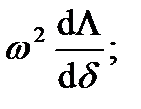 Р =
Р = 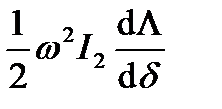 . (5-19)
. (5-19)
Здесь произведение w I представляет собой МДС F 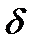 , приложенную к воздушному зазору. В таком случае
, приложенную к воздушному зазору. В таком случае
P =  . (5-20)
. (5-20)
Для электромагнитных систем, работающих при постоянном потокосцеплении  = const, d
= const, d  /d
/d 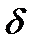 = 0 и
= 0 и
P =  . (5-21)
. (5-21)
Так как I =  ;
;  = -
= - 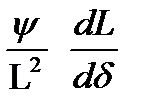 ;
;  =
=  , то
, то
P = 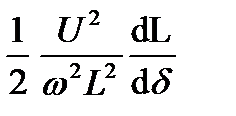 . (5-22)
. (5-22)
Заменив в формуле (5-22) U/w = Ф w J/  , a L=
, a L= 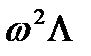 , получим
, получим
P = 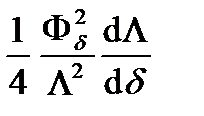 . (5-23)
. (5-23)
С учетом рассеяния
P = 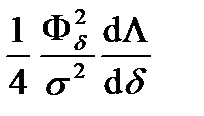 . (5-24)
. (5-24)
Таким образом, уравнения (5-20) и (5-24) позволяют определить тяговые усилия для электромагнитов постоянного и переменного тока.
Для построения тяговых характеристик, кроме зависимостей F 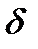 = f(
= f(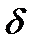 ) или
) или
Ф = f(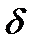 ), необходимо иметь вспомогательные кривые:
), необходимо иметь вспомогательные кривые:  = f(
= f(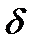 ) /(8);
) /(8); 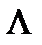 = f(
= f(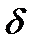 );
);
d 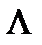 /d
/d 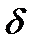 =f(
=f( 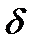 ) ).
) ).
Сила притяжения электромагнита может быть вычислена по формуле Максвелла:
Р = В 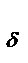 2S
2S 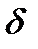 (2
(2 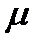 0), (5-25)
0), (5-25)
где В 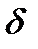 — индукция в рабочем зазоре; S
— индукция в рабочем зазоре; S 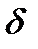 - эквивалентное сечение воздушного зазора;
- эквивалентное сечение воздушного зазора; 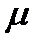 0 - магнитная проницаемость воздуха.
0 - магнитная проницаемость воздуха.
Формулой (5-25) можно пользоваться, если индукция в воздушном зазоре распределена равномерно. При неравномерном распределении индукции воздушный зазор можно разбить на отдельные параллельные участки  S
S 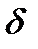 и, принимая индукцию равномерной на каждом участке, вычислить силу притяжения как сумму сил отдельных участков. Формулой (5-25) можно также пользоваться, если достаточно точно определена средняя индукция.
и, принимая индукцию равномерной на каждом участке, вычислить силу притяжения как сумму сил отдельных участков. Формулой (5-25) можно также пользоваться, если достаточно точно определена средняя индукция.
При однородном магнитном поле
Р = 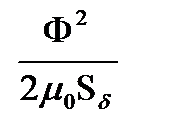 . (5-26)
. (5-26)
Поиск по сайту: