Динамічні системи

Послідовна зміна станів системи, зображена у вигляді точок у просторі станів, називається фазовою траєкторією, а простір станів – фазовим простором. Розмірність фазового простору дорівнює числу змінних (координат), які визначають стан системи. Різниця між кількістю змінних і кількістю зв'язків між ними визначає число ступенів свободи системи та визначає кількість незалежних змінних. Область простору станів, у якій може перебувати система називають областю припустимих станів, якщо координати є безперервними величинами. У дискретних системах координати приймають фіксовані значення, простір станів таких систем є дискретним. В області припустимих станів системи перебуває стан, що найбільше відповідає меті та умовам функціонування системи. Такий стан називається нормою стану, тобто функціональним оптимумом. Під оптимальним функціонуванням системи розуміють проходження всіх процесів з найбільш можливою надійністю та економічністю.

Перетворення систем. Зміна стану системи відбувається як під впливом зовнішніх факторів, так і у результаті процесів, що відбуваються всередині самої системи. Позначимо стан системи у даний момент через .

Визначимо основні чинники, що впливають на стан системи: – характеристики системи, які залежать від зовнішнього середовища та зв'язків і не можуть варіюватися довільно – незалежні змінні; – параметри керування, які можуть змінюватися у процесі функціонування системи та використовуються для підвищення її якості. Вплив зовнішнього середовища на систему характеризується вхідними впливами , які розбиваються на дві підмножини: множина керуючих вхідних впливів , з використанням якої здійснюється цілеспрямована зміна стану системи; і множина некерованих вхідних впливів .

Тоді 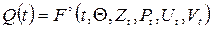, де – початковий (нульовий) стан системи в момент ; – оператор стану.

Позначимо – множину виходів, через які система впливає на зовнішнє середовище. Значення вихідних параметрів залежать від вхідних впливів і внутрішніх характеристик і , тобто , де зміна структури (при необхідності). – оператор виходу. Матеріально-енергетичний або інформаційний обмін між системою та середовищем називається метаболізмом.

– закон функціонування системи. При розгляді функціонування системи вводиться поняття – алгоритм функціонування системи, під яким розуміється метод одержання вихідних характеристик з урахуванням вхідних впливів зовнішнього середовища та змін характеристик, параметрів і структури системи. Один і той же закон функціонування системи може бути реалізований різними способами, тобто за допомогою різних алгоритмів функціонування.

Модель системи у самому загальному вигляді можна представити наступним виразом .

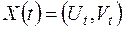Функціонування системи може відбуватися у стаціонарному, перехідному і періодичному режимах. Якщо стан системи не змінюється – то режим стаціонарний, якщо він змінюється під зовнішнім впливом і повертається у стаціонарний режим через деякий період – то режим перехідний. Запишемо спрощено перехідний процес, позначимо – вектор станів; – вектор входів; – вектор виходів; – час.

Тоді динамічні властивості системи задаються

, (5)

а відповідно вихідні характеристики:

. (6)

Для характеристики здатності системи повертатися до стану рівноваги або змінювати стаціонарний режим під дією зовнішнього впливу використовують поняття чутливості та стійкості.

Чутливість стану системи це реакція системи на вхідний вплив: 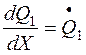, а чутливість виходу характеризується похідною .

Якщо стан системи зберігається незалежно від зовнішніх порушень, це свідчить про її стійкість.

Стійкість – це здатність системи прагнути з різних початкових станів до деякого рівноважного (стаціонарного режиму).

Для оцінки стійкості динамічних систем використається поняття стійкості за Ляпуновим. Для лінійних систем, що описуються системою лінійних диференціальних рівнянь: , (де А та В – матриці коефіцієнтів) стійкість оцінюється критеріями Рауса, Гурвіца. Стійкість є позитивною характеристикою системи, але іноді вона не допускає гнучкості у керуванні. Через стійкість можна ввести поняття інваріантності системи.

Інваріантність у послідовності станів системи полягає в тому, що не дивлячись на зміни, які відбуваються у системі в цілому, деякі її властивості залишаються незмінними. Такий аналіз необхідний для керування функціонуванням системи в умовах випадкових або навмисних збурень. Наприклад: чи варто затрачати зусилля на повернення системи у стаціонарний режим, або вона сама повернеться, а які зовнішні збурення повинні бути обов'язково ліквідовані і т. ін.

Поиск по сайту: