Энергетический баланс химико-технологических процессов

Эффективность использования энергии при осуществлении химико-технологического процесса устанавливается с помощью энергетического баланса. Основой его служит закон, математическая формулировка которого имеет вид [9]

где Е – энергия; m – масса; с – скорость света в вакууме.

Чаще для химико-технологических процессов ограничиваются составлением теплового баланса, отнеся его к тем единицам, которые использовались для составления материального баланса.

Если при проведении процесса энергия может подводиться или отводиться в иной форме, чем тепловая, то в общем балансе она учитывается с помощью соответствующих эквивалентов теплоты.

В таком балансе количества энергии, подведенные к системе и полученные в результате превращений (приход тепла), должны быть равны количествам, которые расходуются на проведение отдельных этапов процесса, преобразовываются в другие виды энергии и отводятся из системы материальными потоками, а также теряются в окружающую среду (расход тепла).

На практике часто составление теплового баланса осложнено неадиабатностью процесса, различием температур реагентов, нестехиометричностью, присутствием инертных газов и неполнотой протекания процесса. В связи с этим рассмотрим два примера.

Допустим, что Т _исх ¹ Т _прод (рис. 12). Тогда процесс можно представить происходящим в несколько стадий: реакция осуществляется при Т _исх, а затем продукты нагреваются до Т _прод (рис. 12, а) или вначале нагреваются исходные вещества, после чего проводят процесс (рис. 12, б). Возможен и такой вариант: охлаждают (нагревают) исходные вещества до некоторой температуры Т ₀, проводят при ней реакцию, после чего продукты реакции нагревают (охлаждают) до Т _прод (рис. 12, в). Хотя последний путь сложнее предыдущих, однако он предпочтительнее, если в качестве Т ₀ выбрать 298,15 К. Вычисления упрощаются, если известны средние теплоемкости всех реагентов в рассчитываемом интервале температур.

Очевидно, что для схемы в можно записать следующее уравнение:

(40)

Т _прод

Т _исх

Т ₀

а б в

Рис. 12. Схема возможных путей протекания реального процесса:

а –; б –; в –

Здесь первое слагаемое представляет изменение энтальпии при переходе всех исходных веществ (включая и инертные газы, если они присутствуют в исходной смеси) от температуры Т _исх входа их в реакционную зону до температуры Т ₀ начала отсчета энтальпии; второе слагаемое равно тепловому эффекту реакции при Т ₀ в расчете на 1 моль вещества (на которое ведется вычисление) и с учетом степени превращения х; третье слагаемое – это изменение энтальпии при нагревании всех веществ, покидающих зону реакции (продукты реакции, инертные вещества и непрореагировавшие исходные вещества). Если в процессе изменения температуры не происходит фазовых превращений, то все D Н _пр будут равны нулю. Если же фазовые превращения имеют место, то для упрощения расчета их можно отнести к Т ₀.

Для составления теплового баланса необходимо знать теплоемкости участвующих в процессе веществ, тепловые эффекты химических реакций (из термохимических расчетов) и теплоты фазовых преобразований.

В технологических расчетах используются значения молярной (С _р(м)) или удельной (С _р) теплоемкости. Молярные теплоемкости равны

.

Удельные теплоемкости соответственно равны

,

где М – молярная масса, г/моль или кг/кмоль.

Когда n молей вещества обмениваются с окружающей средой Q кДж теплоты, и при этом температура вещества изменяется от Т ₁ до Т ₂, то средняя молярная теплоемкость при постоянном давлении (1) или объеме (2) равна

. (41)

Зависимость молярной теплоемкости от температуры выражается с помощью эмпирических уравнений

С _р(м) = а + bT + cT ² + dT ³,

C _p(м) = a + bT + , (42)

где а, b, c, d – характерные для данного вещества постоянные (число членов зависит от требуемой степени точности и величины температурного интервала).

Для составления тепловых балансов процессов, для которых в широких пределах изменяется температура (например, процессов горения), нужно знать зависимость молярной теплоемкости веществ, участвующих в этом процессе, от температуры. Уравнения (42) дают возможность рассчитать истинные молярные теплоемкости при данной температуре. Если же вещество нагревается или охлаждается в широком интервале температур, то обычно в таких случаях определяется средняя молярная теплоемкость для данного диапазона температур.

Значения молярной теплоемкости некоторых газов приведены в табл. 10. Размерность теплоемкости в справочных таблицах может быть представлена в виде кал/(моль × град); Дж/(моль × К); кДж/(кмоль × К); кДж/(кг × К); кДж/(м³ × К). Размерность теплоемкости должна соответствовать размерности слагаемых членов уравнения теплового баланса.

Теплоемкость смеси – аддитивное свойство теплоемкостей составляющих ее компонентов С _р(м):

, (43)

где N_i = n_i / .

Температура потоков в элементах ХТС изменяется за счет внутренних источников, одним из которых являются химические превращения.

Количество теплоты, которое выделяется или поглощается в результате реакции, вычисляется из термохимического уравнения

n _а А + n _b B + … = n _r R + n _s S + … + Q (-D Н), (44)

где Q – тепловой эффект реакции; D Н - энтальпия реакции.

Тепловой эффект Q и энтальпия D Н реакции противоположны по знаку (Q = -D Н).

Стандартные тепловые эффекты химических реакций могут быть рассчитаны на основе теплот образования веществ, участвующих в реакции, согласно следствию из закона Гесса. Теплоты образования веществ приведены в соответствующих справочниках. При этом в качестве стандартных условий приняты температура 298 К, давление 1 атм (101,325 кПа) и для растворенных веществ – концентрация 1 моль/кг растворителя. Газы и растворы предполагаются идеальными.

Значение теплового эффекта в уравнении (44) зависит от записи химического уравнения. Например, в уравнениях

N₂ + 3H₂ Û 2NH₃ + Q

0,5N₂ + 1,5H₂ = NH₃ + Q

значения Q различаются в 2 раза в соответствии со стехиометрическими коэффициентами. В справочной литературе тепловой эффект приводят для соответствующего уравнения либо при превращении 1 моля или 1 кмоля вещества.

Зависимость теплового эффекта реакции (изменения энтальпии) от температуры следует из закона Кирхгофа

. (45)

Из уравнения следует, что чувствительность D Н к изменению Т определяется абсолютным значением D С _р(м), а знак температурного коэффициента теплового эффекта – знаком D С _р(м). При D С _р(м) > 0 тепловой эффект реакции растет с увеличением температуры, при D С _р(м) < 0 – уменьшается, при D С _р(м) = 0 – не зависит от температуры.

В соответствии с уравнением (42) уравнение (45) можно представить как

, (46)

где приращения Δ а,Δ в,Δ с,Δ d вычисляются как и т. д.

После интегрирования уравнения (46) получим

. (47)

На основе значений стандартных теплот образования можно рассчитать энтальпию реакции D Н 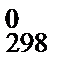при температуре 298 К. Подставив в уравнение (47) значение D Н 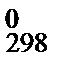и температуру 298 К, найдем постоянную интегрирования I. Из уравнения (47) можно определить энтальпию реакции при любой температуре (в диапазоне, где действительно уравнение (42)).

Пример 1. Рассчитать Δ Н 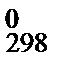для реакции разложения метана при температуре Т = 1000 К:

СН₄ = С + 2Н₂

Поиск по сайту: