ОПРОВЕРЖЕНИЕ ГИПОТЕЗ

Опровержение гипотез осуществляется путем опровержения (фальсификации) их следствий. При этом может обнаружиться, что многие или все необходимые следствия рассматриваемой гипотезы не имеют места в действительности. Кроме того, воз­можно, будут найдены факты, противоречащие выведенным сле­дствиям.

Опровержение гипотез происходит в форме отрицающего мо­дуса (modus tollens) условно-категорического умозаключения, имеющего форму: Этот модус всегда дает достоверное заключение.

Структура опровержения гипотезы такова:

Если имела место причина (гипотеза) Н, то должны быть следствия: С₁ и С₂, и С₃,..., и С _n.

Суждение, что есть следствие С ₁или С₂, или С₃,..., или С _n, является ложным.

_________________

Тогда ложна Н.

В символической логике это умозаключение можно записать таким способом:

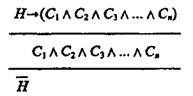
В данном умозаключении мы пользуемся законом де Моргана:

в котором дизъюнкция берется нестрогая. Это означает, что могут отсутствовать одно, два, три или все η следст­вий. Поэтому для наглядности и удобства практического исполь­зования структуру опровержения гипотез путем опровержения (фальсификации) ее следствий лучше записать таким образом:

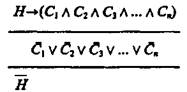При более точном выражении эта структура опровержения совпадает по формуле не с правилом modus tollens, имеющим только одно основание и одно следствие, а с простой деструктив­ной дилеммой, или трилеммой, или полилеммой, в зависимости от того, сколько следствий вытекает из данной гипотезы: два, три или более.

Приведем пример опровержения гипотезы, из которой выте­кают шесть следствий, т. е. пример простой деструктивной поли­леммы.

Если человек болен крупозным воспалением легких, то у него будет высокая температура (39—40°), сильный озноб, частый сухой кашель, боли в боку, одыш­ка, общее тяжелое состояние.

У данного больного нет высокой температуры (39—40°), или нет сильного озноба, или нет частого сухого кашля, или нет болей в боку, или нет одышки, или общее состояние больного не является тяжелым.

_________________________________________________________

Этот человек не болен крупозным воспалением легких.

Чем большее число следствий отсутствует, тем выше степень опровержения высказанной гипотезы. Если бы в приведенном примере отсутствовало лишь одно или два следствия, то нельзя было бы сделать вывод, что человек не болен крупозным вос­палением легких. Здесь опровергаемые (фальсифицируемые) сле­дствия тоже надо брать по возможности в совокупности. Хотя простое отсутствие следствий (или их необнаружение) не опрове­ргает окончательно гипотезу, так как в данное время, при данных обстоятельствах мы могли их не обнаружить, выдвинутая гипо­теза (или версия) будет подвергнута сомнению. Гипотеза окон­чательно опровергается, если обнаруживаются факты, обстояте­льства, явления, противоречащие вытекающим из данной гипо­тезы следствиям.

Поиск по сайту: