АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Неявные определения

Читайте также:
  1. I. Открытые способы определения поставщика.
  2. Алгоритм определения предпочтительной организационной структуры управления диверсифицированной фирмы
  3. АНКЕТА ОПРЕДЕЛЕНИЯ ВОЛЕВЫХ КАЧЕСТВ У УЧАЩИХСЯ 12-16 ЛЕТ
  4. АНКЕТА ОПРЕДЕЛЕНИЯ ВОЛЕВЫХ КАЧЕСТВ У УЧАЩИХСЯ 16 ЛЕТ И СТАРШЕ И СТУДЕНТОВ
  5. АНКЕТА ОПРЕДЕЛЕНИЯ ВОЛЕВЫХ КАЧЕСТВ У УЧАЩИХСЯ 7-12 ЛЕТ
  6. Бальнеология. Понятия и определения
  7. БИАС-тест определения репрезентативных систем
  8. Более результативной с точки зрения определения победите-
  9. Верный способ определения ГПЗ зоны в помещении
  10. Виды кислотности, методы определения и оценки
  11. Виды щелочности, методы определения и оценки
  12. Внесение представлений на противоречащие закону решения, приговоры, определения и постановления судов

Вотличие от явных определений, имеющих структуру 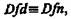в неявных определениях просто на место Dfn подставляется контекст, или набор аксиом, или описание способа постро­ения определяемого объекта.

Контекстуальное определение позволяет выяснить содержа­ние незнакомого слова, выражающего понятие, через контекст, не прибегая к словарю для перевода, если текст дан на иностран­ном языке, или к толковому словарю, если текст дан на родном языке.

Значения неизвестных в уравнениях даны в неявном виде. Если дано уравнение, первой степени, например 10— y =3, или дано квадратное уравнение, например х 2 — 7 x +12=0, то, решая их и находя значение корней этих уравнений, мы даем явное определение для у (у =7) и для х (x1 = 4 и х2 = 3).

Индуктивные определения характеризуются тем, что определя­емый термин используется в выражении понятия, которое ему приписывается в качестве его смысла. Примером индуктивного определения является определение понятия «натуральное число» с использованием самого термина «натуральное число»:

1.1 — натуральное число.

2. Если n — натуральное число, то n + 1 — натуральное чи­сло.

3. Никаких натуральных чисел, кроме указанных в пунктах 1 и 2, нет.

С помощью этого индуктивного определения получается на­туральный ряд чисел: 1, 2, 3, 4.....Таков алгоритм построения натуральных чисел.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)