 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
СРЕДНИЕ ВЕЛИЧИНЫ
Имеются следующие данные о лабораторных испытаниях 1000 образцов пряжи на крепость
| Крепость пряжи, г | Число образцов |
| до 180 | |
| 180-200 | |
| 200-220 | |
| 220-240 | |
| 240 и более |
Средняя крепость пряжи составляет:
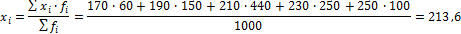
Ответ: 213,6.
Пример 1.
Имеются следующие данные о производстве рабочими продукции А за смену:
| № раб. | ||||||||||
| Выпущено изделий за смену |
В данном примере варьирующий признак - выпуск продукции за смену.
Численные значения признака (16, 17 и т. д.) называют вариантами. Определим среднюю выработку продукции рабочими данной группы:
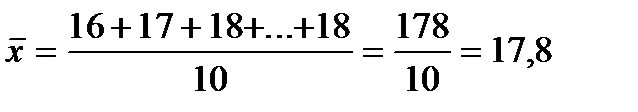
Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т.е. данные не сгруппированы. Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе.
Пример 2.
Имеются следующие данные о заработной плате рабочих - сдельщиков:
| Месячная з/п (варианта - х), руб. | Число рабочих, n | xn |
| х = 110 | n = 2 | |
| х = 130 | n = 6 | |
| х = 160 | n = 16 | |
| х = 190 | n = 12 | |
| х = 220 | n = 14 | |
| ИТОГО |
По данным дискретного ряда распределения видно, что одни и те же значения признака (варианты) повторяются несколько раз. Так, варианта х встречается в совокупности 2 раза, а варианта х-16 раз и т.д.
Число одинаковых значений признака в рядах распределения называется частотой или весом и обозначается символом n.
Вычислим среднюю заработную плату одного рабочего 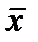 в руб.:
в руб.:
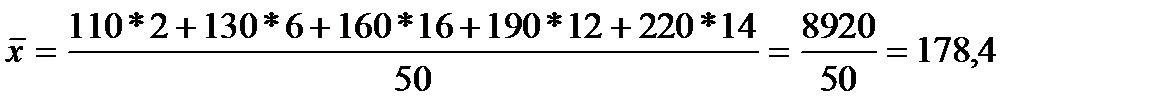
Фонд заработной платы по каждой группе рабочих равен произведению варианты на частоту, а сумма этих произведений дает общий фонд заработной платы всех рабочих.
В соответствии с этим, расчеты можно представить в общем виде:
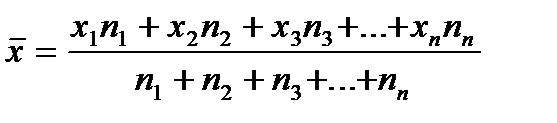
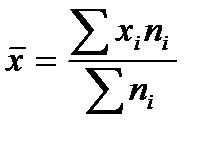
Полученная формула называется средней арифметической взвешенной.
Из нее видно, что средняя зависит не только от значений признака, но и от их частот, т.е. от состава совокупности, от ее структуры. Изменим в условии задачи состав рабочих и исчислим среднюю в измененной структуре.
Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или открытыми интервалами.
Рассмотрим расчет средней арифметической для таких рядов.
Пример 3.
Имеются следующие данные:
| Группы рабочих по количеству произведенной продукции за смену, шт. | Число рабочих, n | Середина интервала, х | хn |
| 3 — 5 | |||
| 5 — 7 | |||
| 7 — 9 | |||
| 9 — 11 | |||
| 11 — 13 | |||
| ИТОГО |
Исчислим среднюю выработку продукции одним рабочим за смену. В данном ряду варианты осредняемого признака (продукция за смену) представлены не одним числом, а в виде интервала "от - до". Рабочие первой группы производят продукцию от 3 до 5 шт., рабочие второй группы - от до 7 шт. и т. д. Таким образом, каждая группа ряда распределения имеет нижнее и верхнее значения вариант, или закрытые интервалы. Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной:
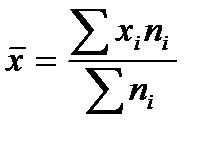
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так, для первой группы дискретная величина х будет равна:
(3 + 5) / 2 = 4
Дальнейший расчет производится обычным методом определения средней арифметической взвешенной:
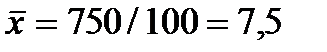
Итак, все рабочие произвели 750 шт. изделий за смену, а каждый в среднем произвел 7,5 шт.
Преобразуем рассмотренный выше ряд распределения в ряд с открытыми интервалами.
Пример 4.
Имеются следующие данные о производстве продукции за смену:
| Группы рабочих по количеству произведенной продукции за смену, шт. | Число рабочих, n | Середина интервала, х | хn |
| до 5 | |||
| 5 — 7 | |||
| 7 — 9 | |||
| 9 — 11 | |||
| свыше 11 | |||
| ИТОГО |
В таких рядах условно величина интервала первой группы принимается равной величине интервала последующей, а величина интервала последней группы - величине интервала предыдущей. Дальнейший расчет аналогичен изложенному выше.
В практике экономической статистики иногда приходится исчислять среднюю по групповым средним или по средним отдельных частей совокупности (частным средним). В таких случаях за варианты (х) принимаются групповые или частные средние, на основании которых исчисляется общая средняя как обычная средняя арифметическая взвешенная.
Пример 5.
Определим средний процент выполнения плана по выпуску продукции по группе заводов на основании следующих данных:
| Номер завода | Выпуск продукции по плану, млн.руб. | Выполнение плана, % |
| ИТОГО | — |
В этой задаче варианты (процент выполнения плана) являются не индивидуальными, а средними по заводу. Весами являются выпуск продукции по плану. При вычислении среднего процента выполнения плана следует использовать формулу средней арифметической взвешенной: 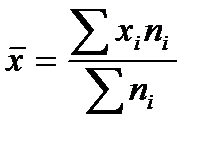 ,
,
где 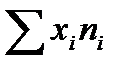 — фактически выпущенная продукция, получаемая путём умножения вариант (процент выполнения плана) на веса (выпуск продукции по плану).
— фактически выпущенная продукция, получаемая путём умножения вариант (процент выполнения плана) на веса (выпуск продукции по плану).
Производя вычисления, варианты (х) лучше брать в коэффициентах.
| или 102,4% |
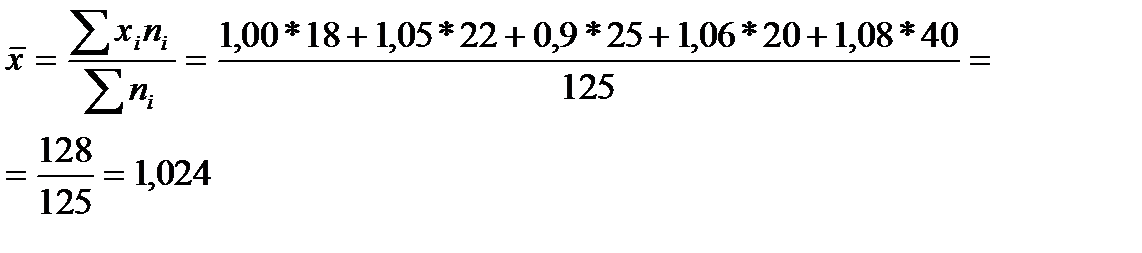
Пример 6.
Бригада токарей была занята обточкой одинаковых деталей в течение 8-часового рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй - 15 мин., третий - 11, четвертый - 16 и пятый - 14 мин. Определите среднее время, необходимое на изготовление одной детали.
На первый взгляд кажется, что задача легко решается по формуле средней арифметической простой:
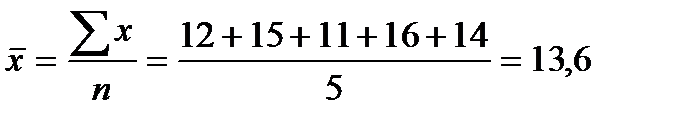
Полученная средняя была бы правильной, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных каждым рабочим, воспользуемся следующим соотношением:
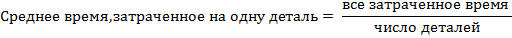
Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали, равно:
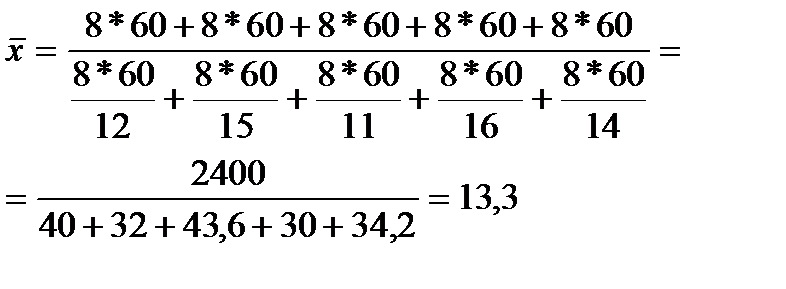
Это же решение можно представить иначе:
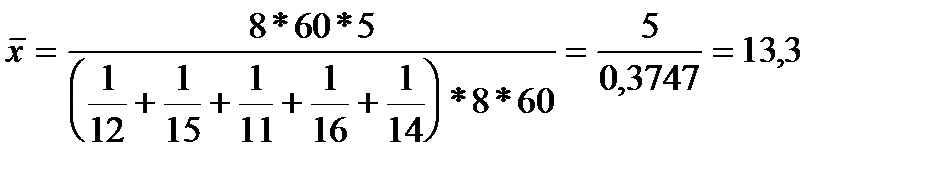
Таким образом, формула для расчета средней гармонической простой будет иметь вид:
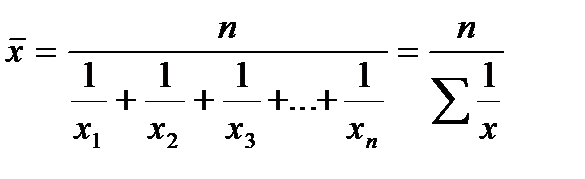
Пример 7.
Издержки производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными:
| Номер завода | Издержки производства, тыс.руб. | Себестоимость единицы продукции, руб. |
Исчислим среднюю себестоимость изделия по трем заводам. Как и прежде, главным условием выбора формы средней является экономическое содержание показателя и исходные данные.
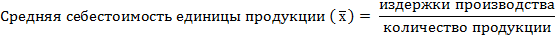
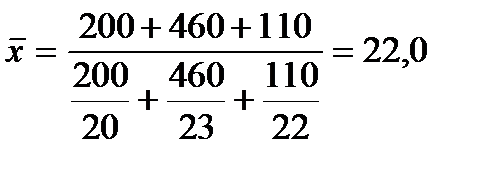 руб.
руб.
Таким образом, формулу для расчета средней гармонической взвешенной можно представить в общем виде:
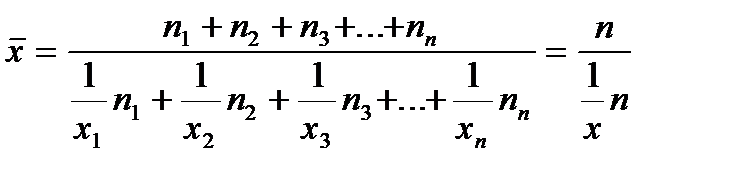
МОДА, МЕДИАНА.
Задача. Имеются данные о распределении 100 семей по количеству детей в семье:
| Число детей | Количество семей |
| Итого |
Мода равна 1.
Пример 8.
Распределение проданной обуви по размерам характеризуется следующими показателями:
| размер обуви | и выше | ||||||||||
| число пар, в % к итогу | — | — |
В этом ряду распределения мода равна 41. Именно этот размер обуви пользовался наибольшим спросом покупателей.
Пример 9.
Распределение предприятий по численности промышленно - производственного персонала характеризуется следующими данными:
| Группы предприятий по числу работающих, чел | Число предприятий |
| 100 — 200 | |
| 200 — 300 | |
| 300 — 400 | |
| 400 — 500 | |
| 500 — 600 | |
| 600 — 700 | |
| 700 — 800 | |
| ИТОГО |
В этой задаче наибольшее число предприятий (30) имеет численность работающих от 400 до 500 человек. Следовательно, этот интервал является модальным интервалом ряда распределения.
Введем следующие обозначения:
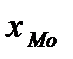 =400,
=400, 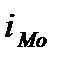 =100,
=100, 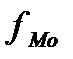 =30,
=30, 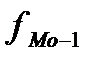 =7,
=7, 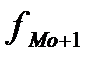 =19
=19
Подставим эти значения в формулу моды и произведем вычисления:
| чел. |
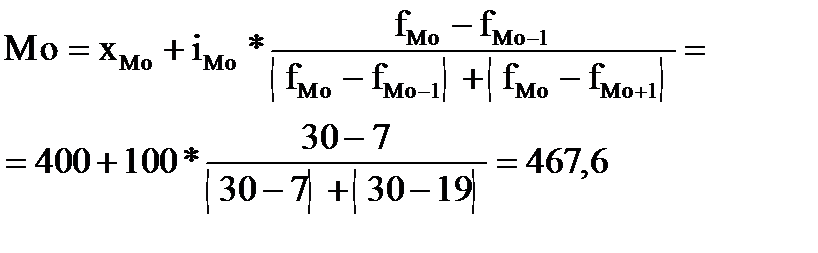
Пример 10.
Определим медиану заработной платы рабочих.
| Месячная з/п, руб. | Число рабочих | Сумма накопительных частот |
| 8 (2+6) | ||
| 24 (8+16) | ||
| — | ||
| — | ||
Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину. В нашем примере сумма частот составила ее половина - 20.
Накопленная сумма частот ряда получилась равной Варианта, соответствующая этой сумме, т.е. 160 руб., и есть медиана ряда.
Если же сумма накопленных частот против одной из вариант равна точно половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.
Пример 11.
| Месячная з/п, руб. | Число рабочих | Сумма накопительных частот |
| 8 (2+6) | ||
| 20 (8+12) | ||
| — | ||
| — | ||
Медиана будет равна:
Ме = (150 + 170) / 2 = 160 руб.
Пример 12.
| Группы предприятий по числу рабочих | Число предприятий | Сумма накопительных частот |
| 100 — 200 | ||
| 200 — 300 | 4 (1+3) | |
| 300 — 400 | 11 (4+7) | |
| 400 — 500 | 41 (11+30) | |
| 500 — 600 | — | |
| 600 — 700 | — | |
| 700 — 800 | — | |
| ИТОГО |
Определим прежде всего медианный интервал. В данной задаче сумма накопленных частот, превышающая половину всех значений (41), соответствует интервалу 400 - 500. Это и есть медианный интервал, в котором находится медиана. Определим ее значение по приведенной выше формуле.
Известно, что:
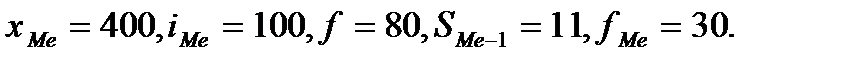
Следовательно,
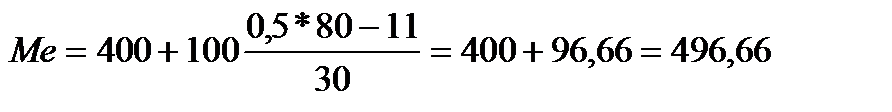
Поиск по сайту: